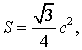 es
decir
es
decir 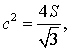 así
que conocido S, obtengamos c.
así
que conocido S, obtengamos c.
Problema 211 de triánguloscabri |
|
547.- Hallar el lado de un triángulo equilátero conociendo su área. Terry y Rivas, A. (1881): Ejercicios de trigonometría. Pedro Abienzo, Impresor del Ministerio de Marina. |
|
Terry y Rivas, A. (1881): Ejercicios
de trigonometría. Pedro Abienzo, Impresor del Ministerio de Marina.
|
Solución de Francisco Javier García Capitán (dedicada a Jose María Pedret).
El área del triángulo equilátero de lado c es 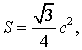 es
decir
es
decir 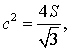 así
que conocido S, obtengamos c.
así
que conocido S, obtengamos c.
 |
|
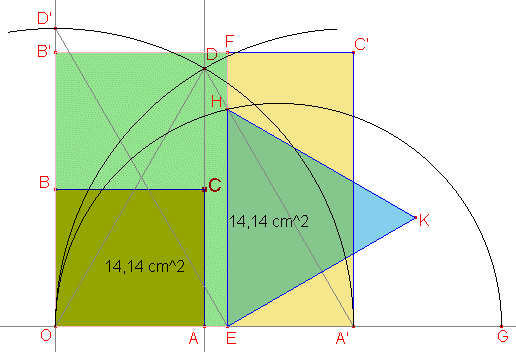
Figura
|
Supongamos que el rectángulo OACB dado tiene área S. Entonces,
hallando los puntos A' y B', simétricos de O respecto A
y B, respectivamente, resultará que el rectángulo OA'C'B'
tiene área 4S. Para dividir este área por Ö3
tendremos en cuenta que la altura de un triángulo equilátero y
la mitad del lado están en la proporción Ö3:1.
Entonces, comenzamos por construir el triángulo equilátero OA'D
sobre OA' y levantar por O una perpendicular a AA', sobre
la que determinamos D' tal que OA' =OD=OD'.
A continuación, trazamos una paralela a A'D por D', que
corta a OA en E. Será OE : OA' = OE
: OD'=AA' : AD=1/Ö3, por
lo que si trazamos la paralela EF a OB', el área de OEFB'
será 4S/Ö3.
Lo que queda es hacer la media geométrica c de los segmentos OE
y EF. Para ello, como es conocido, obtener el punto G sobre OE
tal que EG =EF, trazar la semicircunferencia con diámetro
OG y levantar una perpendicular por E, que cortará en H
a la semicircunferencia, siendo c=EH la media buscada. En la figura,
hemos trazado un triángulo equilátero sobre EH y hemos
comprobado con Cabri que tiene la misma área que el rectángulo
OACB.