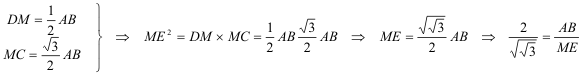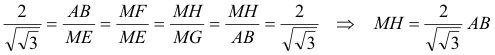Problema 211 547.- Hallar el lado de un triángulo equilátero conociendo su área. Terry y Rivas, A. (1881): Ejercicios de trigonometría. Pedro Abienzo, Impresor del Ministerio de Marina. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat. 17 de enero de 2005 |
|
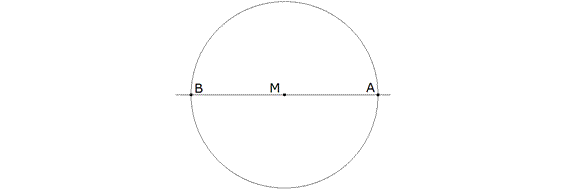
Figure 1 Sea S el área del triángulo y sea AB un segmento tal que AB2 = S Sea M el punto medio de AB. Con diámetro AB trazamos el círculo de centro M. |
|
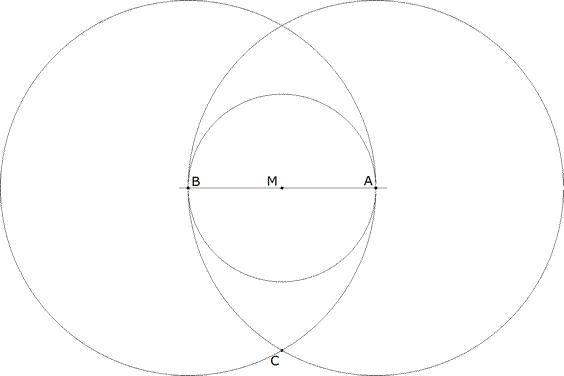
Figure 2 Con centro en A trazamos un círculo de radio AB. Con centro en B trazamos un círculo de radio AB. Estos últimos círculos se cortan en C. |
|
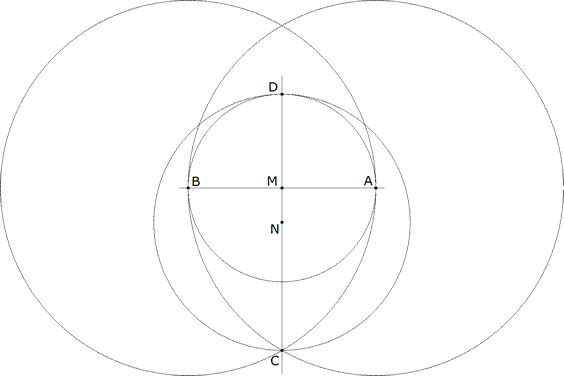
Figure 3 Trazamos MC que corta en D al círculo de diámetro AB. Sea N el punto medio de CD. Con centro en N trazamos el círculo de diámetro CD. |
|
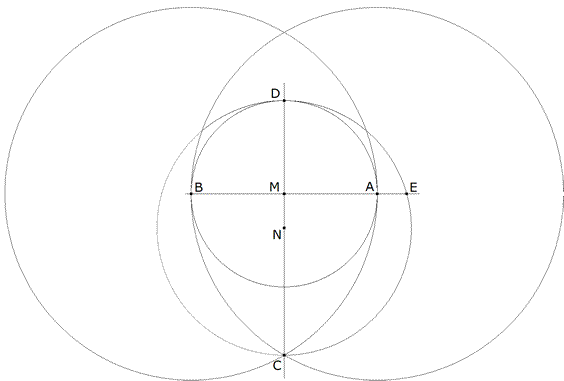
Figure 4 Este último círculo corta a AB en E.
|
|
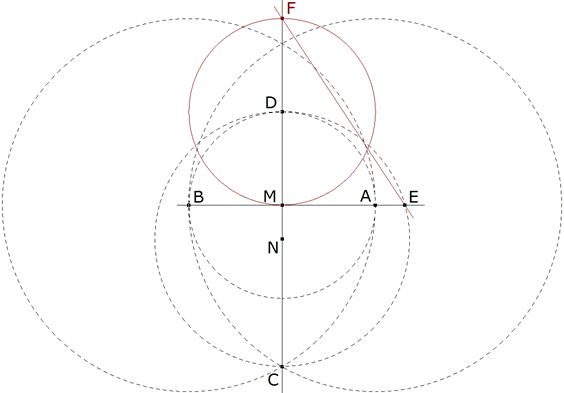
Figure 5 Con centro en D trazamos el círculo de radio DM = AM que corta a CD en F. La recta EF define la proporción entre AB y ME. |
|
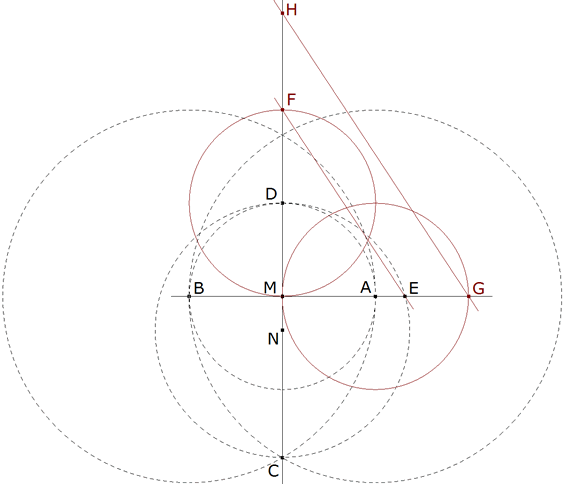
Figure 6 Con centro en A trazamos el círculo de radio AM que corta a AB en G. La paralela a EF por G corta en H a CD. MH ES EL LADO DEL TRIANGULO EQUILATERO BUSCADO
y en un triángulo equilátero de lado MH el área es
 |