Para el aula

Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid)

Problema 212

Problema 731: Sea el triángulo ABC rectángulo en A, tracemos los círculos inscrito y circunscrito.

Sean M y N los puntos de tangencia del primero con los lados AB y AC.

Tracemos la tangente al circunscrito en el punto A.

Esta tangente y la recta MN se cortan en un punto K.

Hallar la distancia AK, siendo los catetos AB=4m y AC=3m

A. M. De Ingenieros Aeronáuticos. (1949). Ejercicios Propuestos de la Gaceta Matemática 1ª Serie, Tomo 1 Madrid (7 de Abril) Instituto "Jorge Juan" de matemáticas y Real Sociedad Matemática Española. Consejo Superior De Investigaciones Científicas, Patronato "Alfonso el Sabio". (Madrid)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat.

1 de febrero de 2005

La solución que presento a continuación no es mía, es la que presenta, con el número 719, JUAN SAPIÑA BORJA en su libro PROBLEMAS GRAFICOS DE GEOMETRIA , LITOGRAF, Madrid marzo de 1955. Y a la que añado la explicación.

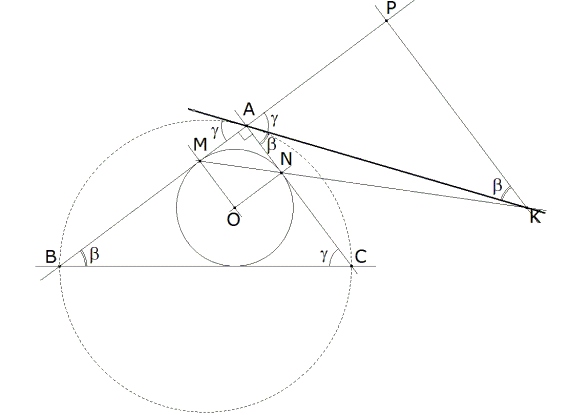
Figura 1

Dibujamos el enunciado y observamos BC=5 (triángulo pitagórico de catetos 4 y 3).

Por K, trazamos una paralela a CA que corta a AB en P.

ΔAMN y ΔPMK son semejantes y como AM=AN ⇒ PK=PM.

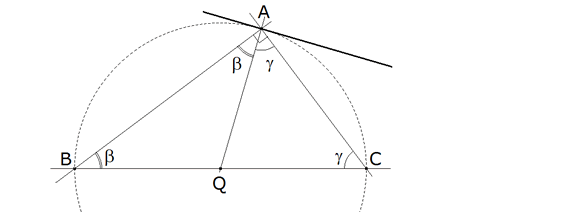
Figura 2

Más difícil es ver que ΔABC y ΔPKA son semejantes gracias a la igualdad de sus tres ángulos: Sea Q el punto medio de BC, QA es perpendicular a AK y QB, QA, QC son iguales; entonces ΔABQ y ΔAQC son isósceles. Los ángulos en el punto A nos permiten determinar todos los ángulos de la figura 1.

A partir de aquí, aplicando propiedades de las proporciones:

Calculemos ahora AM a través del área de ABC, utilizando que AM=r, radio circunscrito.

Sustituyendo estos valores en la proporción anterior