Problema 212
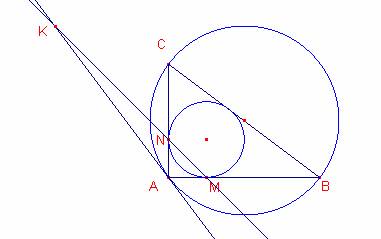
Problema 731: Sea el triángulo ABC rectángulo en A, tracemos los círculos inscrito y cincunscrito.
Sean M y N los puntos de tangencia del primero con los lados AB y AC.
Tracemos la tangente al circunscrito en el punto A.
Esta tangente y la recta MN se cortan en un punto K.
Hallar la distancia AK, siendo los catetos AB=4m y AC=3m
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) :
Aplicando el teorema de Pitágoras al triángulo rectángulo ![]() :
:
![]() .
.
Aplicando razones trigonométricas al triángulo rectángulo ![]() :
:
![]() .
.
Por ser el ángulo ![]() semiinscritoo al círculo circunscrito mide la mitad del arco que abarca. Por tanto:
semiinscritoo al círculo circunscrito mide la mitad del arco que abarca. Por tanto:
![]() .
.
Por ser M y N los puntos de tangencia del triángulo ![]() con el círculo inscrito:
con el círculo inscrito:
![]()
El triángulo ![]() es isósceles.
es isósceles.
![]()
Aplicando el teorema de los senos al triángulo ![]() :
:
![]()
Entonces:
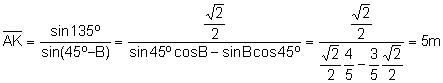 .
.