|
Para el aula Propuesto por Maite Peña Alcaraz,
estudiante de Industriales en Problema 212 Problema 731: Sea el triángulo ABC rectángulo en A, tracemos los círculos inscrito y cincunscrito.
Sean M y N los puntos de tangencia del primero con los lados AB y AC. Tracemos la tangente al circunscrito en el punto A. Esta tangente y la recta MN se cortan en un punto K. Hallar la distancia AK, siendo los catetos AB=4m y AC=3m A. M. De Ingenieros Aeronáuticos. (1949). Ejercicios Propuestos de |
Solución de Ricardo Linares Saldaña (estudiante de
Trujillo-Perú)
rikrdo_89@hotmail.com
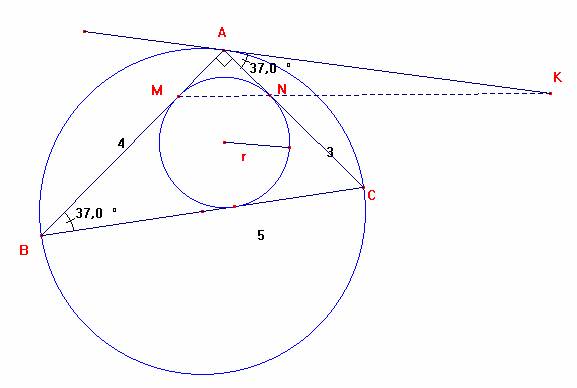
Distancia AK = x, AB =
El triángulo ABC es notable de 37 y 53.
Aplicamos Poncelet entonces 4+3
= 2r + 5, y r = 1, AM = 1, AN = 1.
El angulo KAC = ABC = 37 °
El triángulo AMG
es notable de 82 y 8
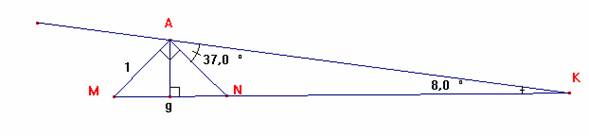
y AG = Ö2/2
triangulo notable x = 5Ö2. Ö2/2
entonces x =5.