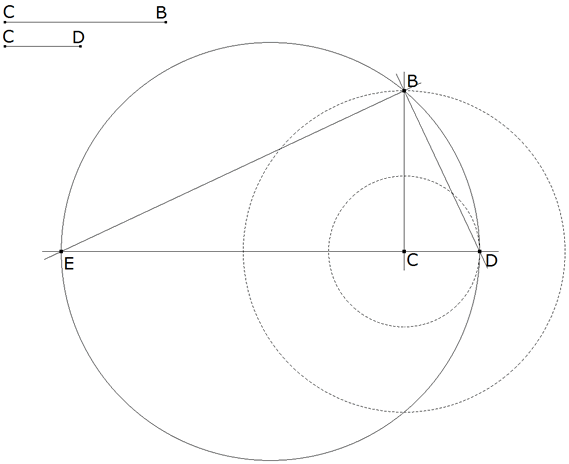Problema 213

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Construir un triángulo rectángulo conocidos un cateto y la diferencia de la hipotenusa con el otro cateto.

González, O. (2005). Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat.

1 de febrero de 2005

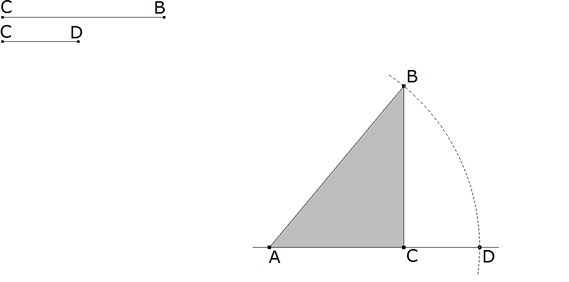
Figura 1

Sea ABC el triángulo rectángulo con la notación puesta de manifiesto en la figura.

Sea a=BC el cateto conocido. Sea b=CA el otro cateto. Sea c=AB la hipotenusa

Sea CD=c-b la diferencia conocida.

Para todo triángulo rectángulo se cumple el teorema de Pitágoras.

a²+b²=c² ⇒ a²=c²-b2=(c-b)(c+b) ⇒ BC²=CD(c+b)

hemos convertido el problema en hallar uno de los factores de un producto conocido el otro factor.

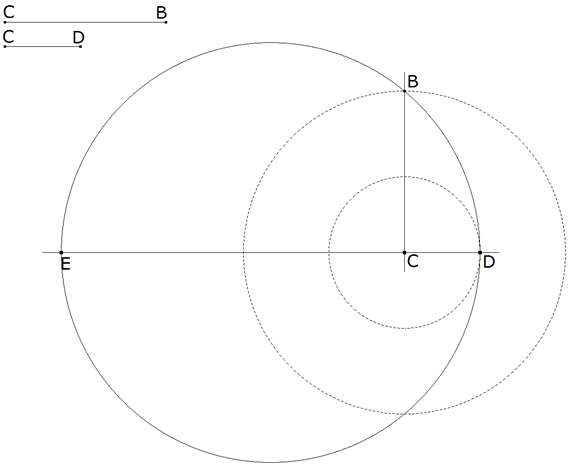
Figura 2

Trazamos CD=c-b.

Por la perpendicular a CD trazamos CB=a.

Si B está sobre el círculo de diámetro ED, es el vértice de un ángulo recto.

ED=EC+CD=(c+b)+(c-b)=2c sería el diámetro del círculo sobre el que se encuentra B.

Figura 3

Si B es el vértice de un ángulo recto trazamos BD.

BE es perpendicular a BD y E su intersección con CD.

Como hemos dicho ED=2c.

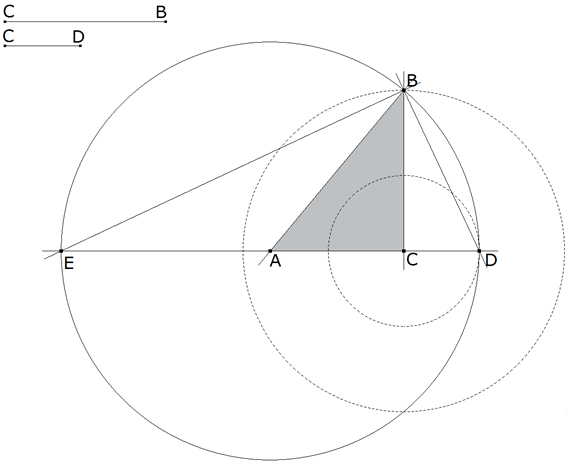
Figura 4

Trazamos A punto medio de ED.

ABC es el triángulo pedido.