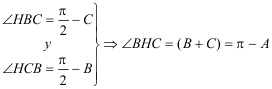Propuesto por José Martel Moreno, profesor emérito de la Universidad de Las Palmas de Gran Canaria

 

Problema 214

Dado un triángulo ABC, hallar el lugar geométrico del ortocentro cuando A recorre una recta no paralela al segmento BC.
 

Martel, J. (2001): Lugares geométricos relacionados con un triángulo cuyos vértices son puntos de una curva plana cualquiera.

En Socas, M., Camacho, M, Morales, A. (Eds). Formación del profesorado e investigación en educación matemática III. Didáctica de las Matemáticas. Departamento de Análisis Matemático. Universidad de La Laguna. (154)

 

Solución de José Maria Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

1 de febrero de 2005.
 
Este problema ya fue resuelto en el número 193. Aunque ahora la recta no es paralela al lado BC, y eso introduce una variación en la resolución pues H pasa dos veces por infinito, Una vez cuando A está en el punto de infinito y otra vez cuando A está sobre BC.
 
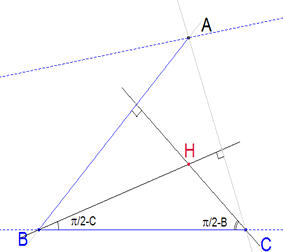01.gif

Observando la figura en la que se representa el ortocentro H de un triángulo ABC vemos que:


ole.gif


Considerando ahora B*, el haz de rectas que pasa por B y considerando C*, el haz de rectas que pasa por C; si estudiamos la transformación h*


ole1.gif

vemos que h* es una proyección de haces de rectas, ya que la intersección de cada recta con su imagen está sobre una recta fija (la no paralela a BC) y por tanto h* es una homografía; lo que significa la relación homográfica

ole2.gif

y por tanto de

ole3.gif

lo que a su vez significa que existe k*:

 

ole4.gif

 

siendo k* una homografía entre haces de rectas donde H es la intersección de las rectas homólogas; pero por el teorema de Chasles Steiner sabemos que el lugar geométrico de la intersección de las rectas homólogas en una homografía de haces de rectas ES UNA CONICA. Analizando un poco más la homografía vemos que cuando el ángulo A→0 el punto A pasa por el punto de infinito de la no paralela a BC, entonces las rectas homólogas coinciden en ∞ (primera vez) y cuando A pasa por la intersección de la recta dada y BC las rectas homólogas coinciden de nuevo en ∞ (segunda vez) por tanto la cónica ES UNA HIPERBOLA.