Problema 214
Proposat per José Martel Moreno, professor emèrit de la Universitat de Las Palmas de Gran Canaria
Donat un triangle ![]() determineu el lloc geomètric de l’ortocentre quan A recorre una recta no paral·lela al segment
determineu el lloc geomètric de l’ortocentre quan A recorre una recta no paral·lela al segment ![]() .
.
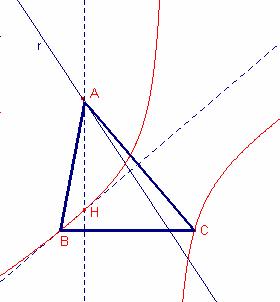
Solució:
Siga la recta ![]()
![]() (r no paral·lela al costat
(r no paral·lela al costat ![]() )
)
Siguen el vèrtexs en les següents coordenades:
![]() (notem que A esta en la recta r).
(notem que A esta en la recta r).
La recta altura al costat ![]() és:
és:
![]()
La recta altura al costat ![]() és:
és:
![]()
L’ortocentre H és la intersecció d’ambdues rectes:
![]()
Per tant el lloc geomètric de l’ortocentre dels triangles ![]() al variar A sobre la recta r recorre la corba:
al variar A sobre la recta r recorre la corba:
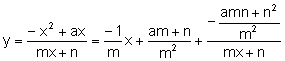
Que té una asímptota horitzontal en ![]() i una asímptota obliqua
i una asímptota obliqua ![]()
Si fem un estudi de la cònica anterior veurem que és una hipèrbola:
![]()
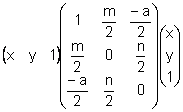
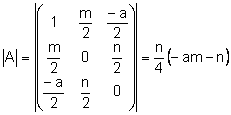
![]() si
si ![]() i
i ![]()
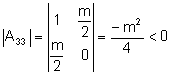 Aleshores la cònica és una hipèrbola.
Aleshores la cònica és una hipèrbola.
Suposem que ![]()
![]()
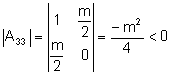
Aleshores la cònica són dues rectes reals no paral·leles
![]() ,
, ![]()
Anàlogament, si ![]()
Suposem que ![]()
![]()
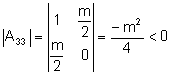
Aleshores la cònica són dues rectes reals no paral·leles.
Fent el mateix estudi si la recta r és paral·lela a ![]() el lloc geomètric de l’ortocentre és una paràbola.
el lloc geomètric de l’ortocentre és una paràbola.