Problema 214

Propuesto por José Martel Moreno, profesor emérito de la Universidad de Las Palmas de Gran Canaria

Dado un triángulo ABC, hallar el lugar geométrico del ortocentro cuando A recorre una recta no paralela al segmento BC.

Martel, J. (2001): Lugares geométricos relacionados con un triángulo cuyos vértices son puntos de una curva plana cualquiera.

En Socas, M., Camacho, M, Morales, A. (Eds). Formación del profesorado e investigación en educación matemática III. Didáctica de las Matemáticas. Departamento de Análisis Matemático. Universidad de La Laguna. (154)

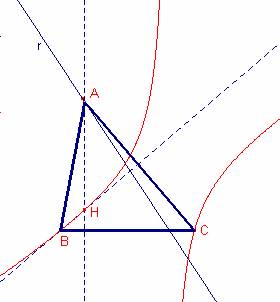
Solución:

Sea la recta (r no paralela al lado )

Sean el vértices en les siguientes coordenadas:

(notemos que A pertenece en la recta r).

La recta altura al lado es:

El ortocentro H es la intersección de ambas rectas:

Por tanto el lugar geométrico del ortocentro de los triángulos al variar A sobre la recta r recorre la curva:

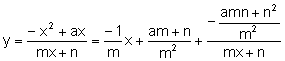
Que tiene una asíntota horizontal en y una asíntota oblicua

Si realizamos un estudio de la cónica anterior veremos que es una hipérbola:

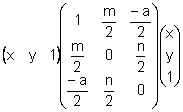
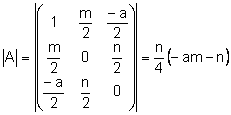
si y

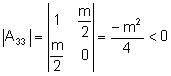Entonces la cónica es una hipérbola.

Supongamos que

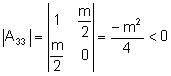
Entonces la cónica son dos rectas reales no paralelas

Análogamente, si

Supongamos que

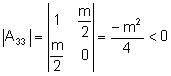
Entonces la cónica son dos rectas reales no paralelas.

Realizando el mismo estudio, si la recta r es paralela a , el lugar geométrico del ortocentro es una parábola.