Problema 215 Sea AD una ceviana cualquiera del triángulo ABC donde D está en el lado BC. Con centro en D, se construyen las dos circunferencias de radios respectivos, DB, y DC, que denotamos por C1 y C2, respectivamente. Sean E y F, los puntos donde las circunferencias C1 y C2 intersecan con la circunscrita C, respectivamente. Probar que : 1) Los puntos E, F y D están alineados. 2) Hallar el lugar geométrico descrito por los puntos E y F, respectivamente, cuando D, varía a lo largo del lado BC. Romero, J.B. (2005): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat. 1 de febrero de 2005 |
|
Analizando el enunciado, vemos que el vértice A sólo sirve para definir el circulo circunscrito Γ. Por lo tanto, dado el segmento BC y un círculo cualquiera Γ que lo tiene como cuerda; si tomamos un punto cualquiera D sobre BC, trazamos el círculo Γ1 de centro D que pasa por B; entonces decimos que Γ ∩ Γ1= E. Trazamos ahora la recta DE que corta a Γ en F, si F está además sobre el círculo Γ2 de centro D y que pasa por C habremos mostrado lo que pide el enunciado en el apartado 1. |
|
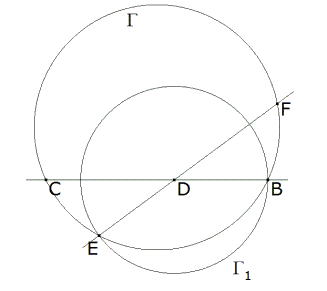
Figura 1
En el círculo Γ, CDxDB=EDxDF. En el círculo Γ1, ED=DB. Sustituyendo, CDxDB=DBxDF ⇒ DC=DF. De lo anterior se deduce que F está sobre el círculo de centro D y radio DC. (c.q.d.) Los puntos E y F, por definición, están siempre sobre el círculo circunscrito; por lo tanto su lugar es el círculo circunscrito Γ. Respondemos así al apartado 2. |