Problema 215.
Proposat per Juan Bosco Romero Márquez, professor col·laborador de la Universidad de Valladolid
Siga 
una ceviana qualsevol del triangle 
(D pertany al costat 
).
Amb centre en D, construïm dues circumferències de radi respectius 
i 
que denotarem per C1 i C2, respectivament.
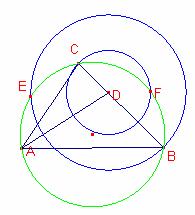Siguen E i F, els punts on les circumferències C1 i C2 intersecten amb la circumferència C3 circumscrita al triangle .
Proveu que:
a) Els punts E, F i D estan alineats.
b) Determineu el lloc geomètric descrit pels punts E, F al variar D al llarg del costat .
Solució de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):
a)
El quadrilàter BFCE està inscrit en la circumferència C3. Siga O el seu centre.
D és el centre de la circumferència C1 la mediatriu a la corda 
passa pels punts O D.
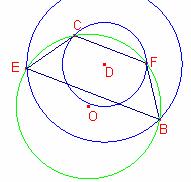D és el centre de la circumferència C2 la mediatriu a la corda 
passa pels punts O, D
La recta que passa pels punts OD és perpendicular a i .
Aleshores i són paral·lels.
Per tant, els segments 
i 
són iguals.
Per tant els triangles 
, 
són iguals.
Aleshores 
.
Aleshores D, E, F estan alineats.
b)
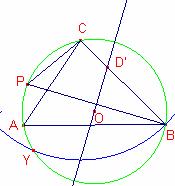Suposem és diàmetre de la circumferència C3 circumscrita, és a dir 
de centre O el punt mig de .
Aleshores el lloc geomètric els tota la circumferència C3. Ja que donat qualsevol punt X de la circumferència C3 les mediatrius a 
i a 
intersecten els costat en O i X pertany a la circumferència de centre O i radi 
.
Suposem que 
, aleshores és menor que el diàmetre de la circumferència C3.
Determinem el lloc geomètric dels punts E del problema.
Considerem la circumferència de centre C que passa per B que talla la circumferència C3 en el punt Y
Vegem que l’arc de circumferència BCY és el lloc lloc geomètric del punt E al variar qualsevol punt D sobre el segment .
Siga P sobre l’arc BCY. 
. 
.
La mediatriu al segment 
talla el segment en D’. La circumferència de centre D’ que passa per B talla la circumferència C3 en P.
Siga P’ en l’arc complementari a BCY.
Tenim que 
.
La mediatriu al segment 
no talla el segment .
Aleshores no existeix D sobre tal que 
.
Anàlogament ho provaríem per a 
.