Problema 215.
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Sea AD una ceviana cualquiera del triángulo ABC donde D está en el lado BC.
Con centro en D, se construyen las dos circunferencias de radios respectivos, DB, y DC, que denotamos por C1 y C2, respectivamente.
Sean E y F, los puntos donde las circunferencias C1 y C2
intersecan con la circunscrita C, respectivamente.
Probar que :
1) Los puntos E, F y D están alineados.
2) Hallar el lugar geométrico descrito por los puntos E y F,
respectivamente, cuando D, varía a lo largo del lado BC.
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):
a)
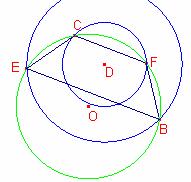
El cuadrilátero BFCE está inscrito en la circunferencia C3. Sea O el centro.
D es el centro de la circunferencia C1 la mediatriz a la cuerda 
pasa por los puntos O D.
D es el centro de la circunferencia C2 la mediatriz a la cuerda 
pasa por los puntos O, D
La recta que pasa por los puntos OD es perpendicular a y .
Entonces y son paralelos.
Por tanto, los segmentos 
y 
son iguales.
Por tanto los triángulos 
, 
son iguales.
Entonces 
.
Entonces D, E, F están alineados.
b)
Supongamos 
es diámetro de la circunferencia C3 circunscrita, es decir 
de centro O el punto medio de .
Entonces el lugar geométrico es toda la circunferencia C3. Ya que dado cualquier punto X de la circunferencia C3 las mediatrices a 
y a 
intersectan los lados en O y X pertenece a la circunferencia de centro O y radio 
.
Supongamos que 
, entonces es menor que el diámetro de la circunferencia C3.
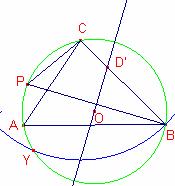
Determinemos el lugar geométrico de los puntos E del problema.
Consideremos la circunferencia de centro C que pasa por B que corta la circunferencia C3 en el punto Y.
Veamos que el arco de circunferencia BCY es el lugar geométrico del punto E al variar cualquier punto D sobre el segmento .
Sea P sobre el arc BCY. 
. 
.
La mediatriz del segmento 
corta el segmento en D’. La circunferencia de centro D’ que pasa por B corta la circunferencia C3 en P.
Sea P’ en el arco complementario a BCY.
Tenemos que 
.
La mediatriz del segmento 
no corta el segmento .
Entonces no existe D sobre tal que 
.
Análogamente lo probaríamos para 
.