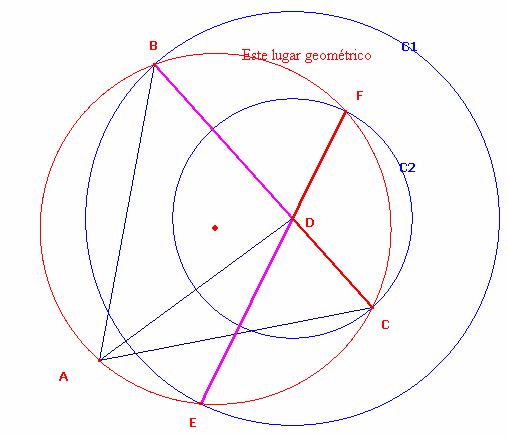
Problema 215

Sea AD una ceviana cualquiera del triángulo ABC donde D está en el lado BC.
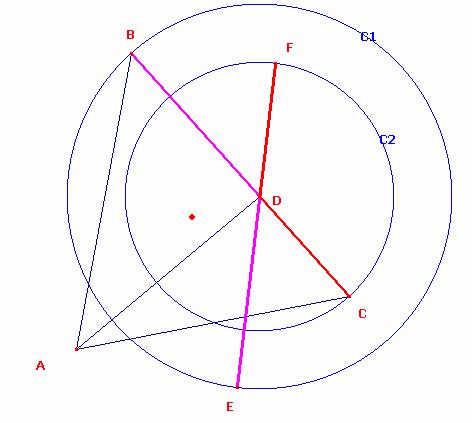
Con centro en D, se construyen las dos circunferencias de radios respectivos, DB, y DC, que denotamos por C1 y C2, respectivamente.
Sean E y F, los puntos donde las circunferencias C1 y C2

Intersecan con la circunscrita C, respectivamente.

Probar que:

1) Los puntos E, F y D están alineados.
Romero, J.B. (2005): Comunicación personal.

Resolución Profesor. William Rodríguez Chamache

Trujillo- Perú

:

 Para demostrar primero aremos algunas demostraciones importantes.

1ro.- observemos la siguiente gráfica

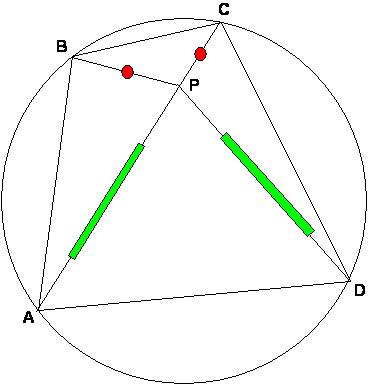
Tenemos un cuadrilátero inscriptible y observamos que los puntos A, P y C son colineales, demostraremos que los puntos B, P  y D también serán colineales y además el cuadrilátero ABCD será  un trapecio isósceles de bases AB y BC .  

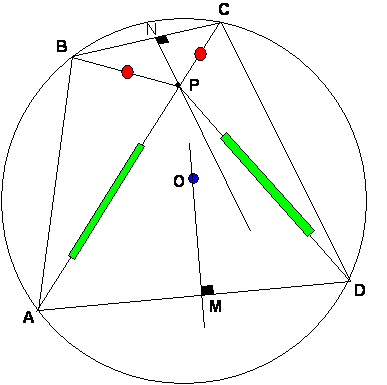
Observamos que al trazar la mediatriz del segmento BC está tendrá que pasar por el punto P y además por el centro O, es decir N, O y P son colineales

De igual manera en el triángulo APD trazamos la mediatriz del segmento AD esta tendrá que pasar  por el punto P y además por el centro O.

Finalmente demostramos que los puntos N, P ,O y M  son colineales  por lo tanto BC y AD son paralelas con lo que se de muestra  que el ABCD es un trapecio y como es inscriptible tendrá  que ser trapecio isósceles donde los lados AB y CD serán iguales

Finalmente la figura correcta será:

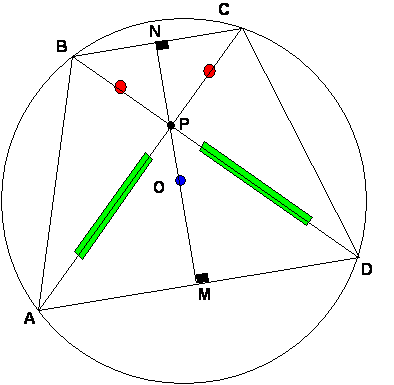
Ahora empecemos la demostración:

En la gráfica observen el cuadrilátero BFCE observamos que es inscriptible 

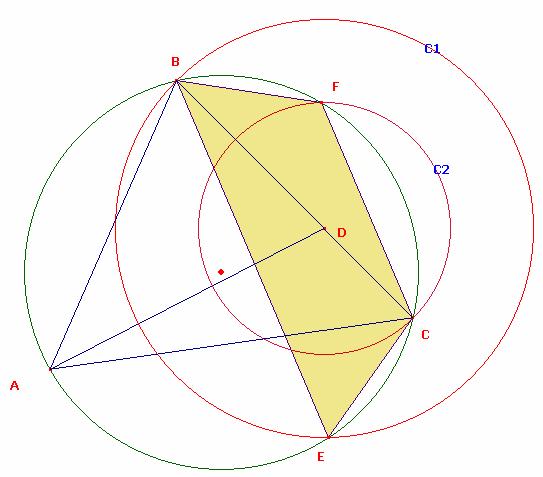
Observemos que en el cuadrilátero se cumple que DB=DE

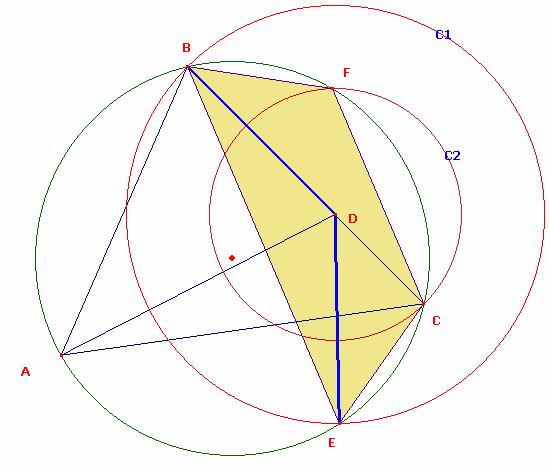
Por otro lado observamos que los segmentos DF=DC

 

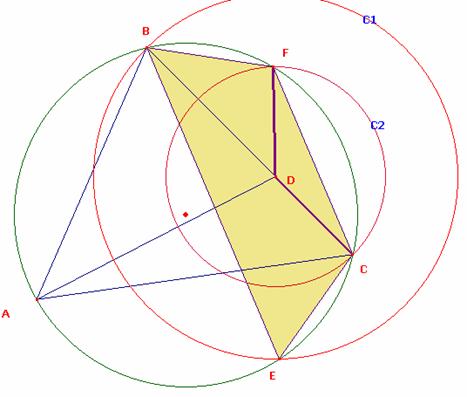
Finalmente obtendremos la siguiente grafica:

Siendo este el caso inicialmente expuesto por lo tanto los puntos E, D y F son colineales 

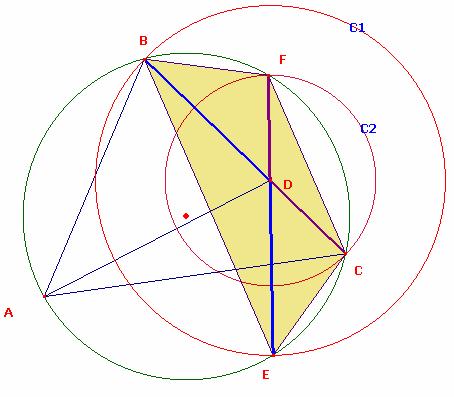
2) Hallar el lugar geométrico descrito por los puntos E y F,
respectivamente, cuando D, varía a lo largo del lado BC.

Resolución:

Como ya demostramos que los puntos E, D y F son colineales, entonces al variar el punto P a lo largo del segmento BC observamos que los segmentos DF y Dc son iguales lo mismo ocurre con los segmentos DB y DE también son iguales por lo tanto al hacer una simple inspección observamos que los productos FD*DE=BD*DC

Es una constante eso nos indica que los puntos pertenecen a una misma circunferencia luego el lugar geométrico  de los punto E y F al variar D por el segmento BC es una circunferencia y cuando D tome el punto medio observaremos que la circunferencia pasa por los punto B y C por lo tanto se trata de la circunferencia circunscrita al triángulo ABC lugar geométrico buscado