Problema 216

Dados dos triángulos homológicos, los puntos de intersección de los lados no homólogos están sobre una misma cónica.

Solución

José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).

1 de febrero de 2005.

0. INTRODUCCION

Enunciamos, en primer lugar, el TEOREMA DE PASCAL y su recíproco. Lo hacemos como en el §64 de Lezioni di geometria proiettiva de Federigo Enriques. Una demostración se puede encontrar en este mismo texto.

De la misma obra §10, exponemos también el PRIMER TEOREMA DE DESARGUES que establece las propiedades de los triángulos homológicos. La demostración se puede hallar en la mayoría de textos de Geometría Proyectiva. Una demostración se puede encontrar en ese mismo texto.

Dibujamos, paso a paso, dos triángulos homológicos; y (sin darnos cuenta) establecemos el resultado propuesto en el enunciado.

1. EL TEOREMA DE PASCAL (1623-1662)

Dice Michel Chasles, en su Aperçu historique...

“... en la obra de Pascal se encuentra el germen de nuevas doctrinas que constituyen lo que se entiende como Geometría Moderna. Por eso hay que tratar con detalle sus descubrimientos.

El más sobresaliente, y que en sus manos parecía “mágico”, es el hermoso teorema del HEXAGRAMA MÍSTICO. El designaba así a esta propiedad de todo hexágono inscrito en una cónica, de tener los tres puntos de concurrencia de sus lados opuestos, siempre en línea recta.

Cinco puntos determinan una cónica; este teorema es pues una relación de la posición de un sexto punto cualquiera de esta curva respecto a los cinco primeros; es pues una propiedad fundamental y característica de las cónicas. También Pascal, que entonces sólo tenía dieciséis años, como el mismo decía lo había convertido en la base para un tratado completo de cónicas. Este tratado no ha llegado a nuestros días; pero parece que Liebnitz en una de sus estancias en París lo tuvo en sus manos y refiere en una carta de 1676 a Perier, sobrino de Pascal, los títulos de las seis partes o tratados que la componían...”

figura.01.gif figura 1

1.1 TEOREMA DE PASCAL - DIRECTO

Si un hexágono simple está inscrito en una cónica, los tres pares de lados opuestos concurren en tres puntos que pertenecen a una misma recta (recta de Pascal); este tipo de hexágono recibe el nombre de hexágono de Pascal.

1.2 TEOREMA DE PASCAL - RECÍPROCO

Todo hexágono de Pascal, en el que tres vértices cualesquiera no están en línea recta, está inscrito en una cónica. Si tres de los vértices están en línea recta, el hexágono está inscrito en un par de rectas (una cónica degenerada)

2. PRIMER TEOREMA DE DESARGUES (1593-1662)

Michel Chasles, en su Aperçu historique... nos dice

“... Desargues, al que Pascal había tomado por guía, iba por delante de una manera nueva y original. Su método, como el de Pascal, reposaba en los principios de la perspectiva y en algunos teoremas de la teoría de transversales. Sólo nos quedan algunas indicaciones poco lúcidas sobre uno de sus escritos titulado Brouillon projet d’une atteinte aux événemens des rencontres du cône avec un plan. Los otros, si han existido, tal como hace suponer un pasaje de l’Essai de Pascal, tal vez se encontraban en hojas sueltas, como las que parece usaba Desargues ya fuera para comunicar sus descubrimientos o fuera para responder a sus numerosos detractores...”

figura.02.gif

figura 2

Dos triángulos sin elementos comunes, situados o no en el mismo plano, y considerándolos referidos el uno al otro:

2.1 TEOREMA DIRECTO

Si los pares de lados homólogos se encuentran respectivamente en tres puntos pertenecientes a una misma recta, las tres rectas que unen los vértices homólogos concurren en un mismo punto.

2.2 TEOREMA RECIPROCO

Si las rectas que unen vértices homólogos se encuentran en el mismo punto, los lados homólogos se encuentran en tres puntos pertenecientes a una misma recta.

2,1 y 2.2 no sólo son teoremas recíprocos, son además correlativos (duales).

3. CONSTRUCCIÓN Y SOLUCION PASO A PASO

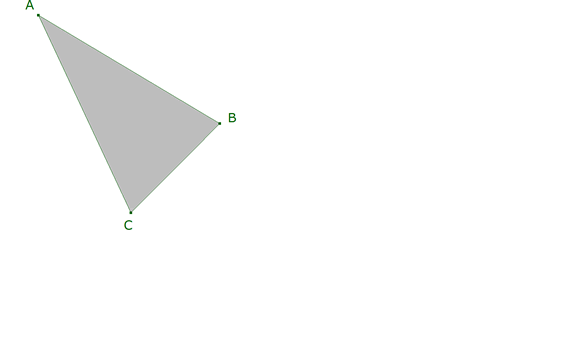
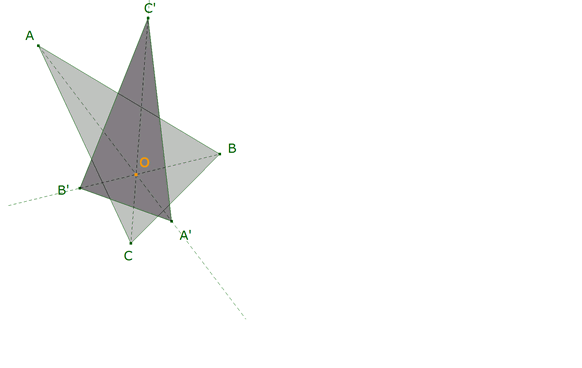
Construimos dos triángulos ABC y A’B’C’ con la condición de que cumplan el TEOREMA DE DESARGUES (triángulos homológicos).

Observando la figura obtenida podemos establecer el resultado buscado.

3.1 PASO 1

figura.03.gif figura 3

Dibujamos un triángulo cualquiera ABC

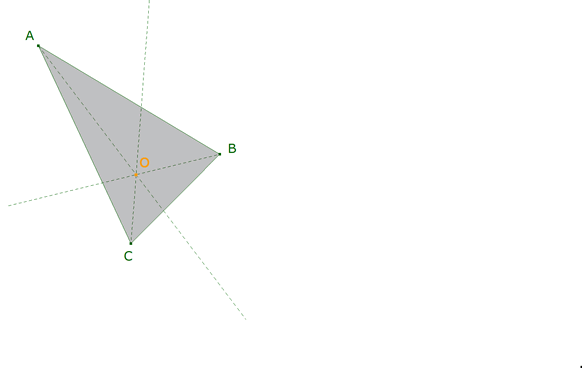
3.2 PASO 2

figura.04.gif

figura 4

Tomamos un punto O cualquiera y trazamos OA, OB, OC.

3.3 PASO 3

figura.05.gif figura 5

Dibujamos ahora los vértices del segundo triángulo A’B’C’. Como los triángulos deben ser homológicos,

O ≡ AA’ ∩ BB’ ≡ BB’ ∩ CC’ ≡ CC’ ∩ AA’ ≡ O,

como nosotros ya conocemos OA, OB, OC debemos tomar los vértices del siguiente modo,

A’ ∈ OA

B’ ∈ OB

C’ ∈ OC

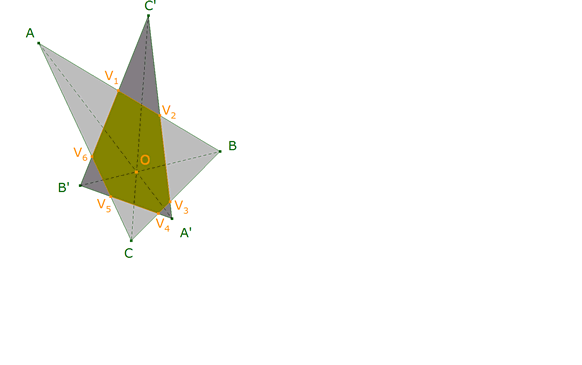
3.4 PASO 4

figura.06.gif figura 6

Hallamos las intersecciones de los lados no homólogos:

V₁ = AB ∩ B’C’

V₂ = AB ∩ C’A’

V₃ = BC ∩ C’A’

V₄ = BC ∩ A’B’

V₅ = CA ∩ A’B’

V₆ = CA ∩ B’C’

Hemos hallado seis puntos que forman el hexágono V₁V₂V₃V₄V₅V₆ y además sus lados cumplen las siguientes identidades (ver figura 6):

V₁V₂≡ AB

V₄V₅ ≡ A’B’

V₂V₃ ≡ C’A’

V₅V₆ ≡ CA

V₃V₄ ≡ BC

V₆V₁ ≡ B’C’

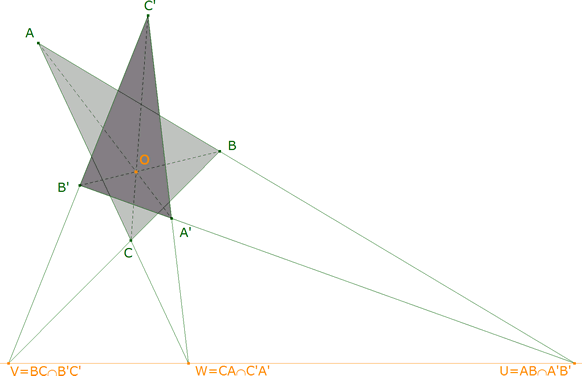
3.5 PASO 5

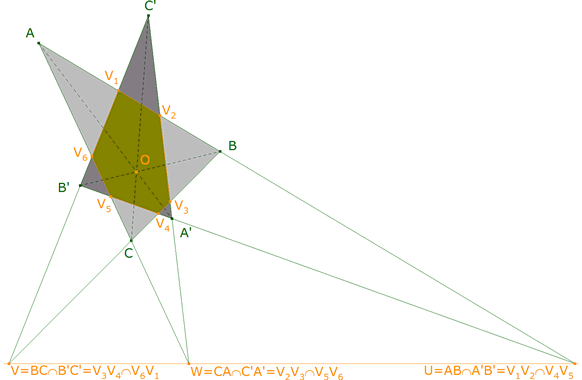
figura.07.gif figura 7

Como las rectas que unen los vértices homólogos concurren en O, los lados homólogos se cortan en puntos que pertenecen a una misma recta:

U = AB ∩ A’B’

V = BC ∩ B’C’

W = CA ∩ C’A’

U, V, W están alineados; pero como hemos visto en el paso anterior podemos escribir

U = AB ∩ A’B’ = V₁V₂ ∩ V₄V₅

V = BC ∩ B’C’ = V₃V₄ ∩ V₆V₁

W = CA ∩ C’A’ = V₂V₃ ∩ V₅V₆

lo que significa que U, V, W son las intersecciones de los lados opuestos del hexágono V₁V₂V₃V₄V₅V₆.

4. LA CONCLUSIÓN

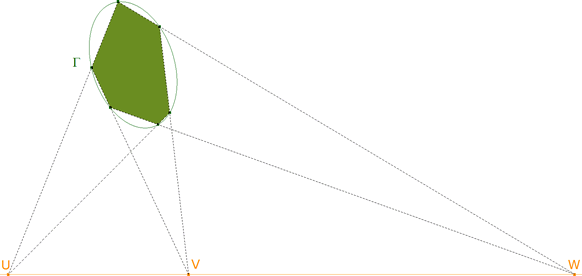
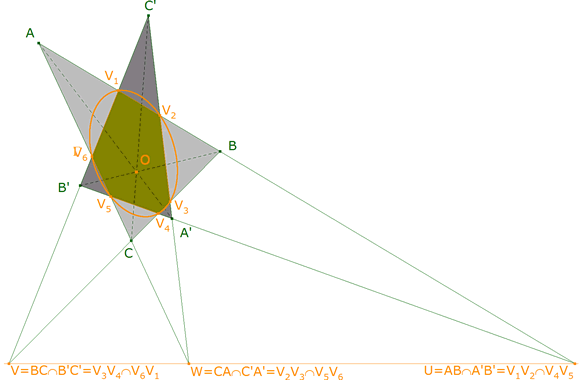
4.1 EL RESULTADO BUSCADO

figura.08.gif figura 8

Como U, V, W están alineados podemos decir que los puntos de intersección de los lados opuestos del hexágono V₁V₂V₃V₄V₅V₆ están alineados y teniendo en cuenta el TEOREMA RECIPROCO DE PASCAL CONCLUIMOS QUE V₁, V₂, V₃, V₄, V₅, V₆ ESTÁN SOBRE UNA MISMA CÓNICA.

C.Q.D.

4.2 UN RESULTADO ADICIONAL

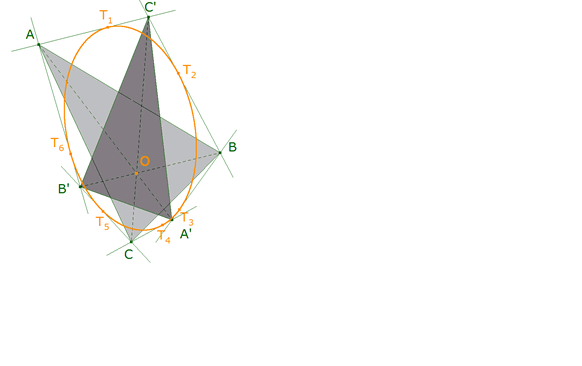
figura.09.gif figura 9

Habiendo probado el enunciado, si escribimos su dual obtenemos

Dados dos triángulos homológicos, las rectas que unen los vértices no homólogos son tangentes a una misma cónica.

Si éste hubiera sido el enunciado, el proceso habría sido igual; pero habría que haber aplicado el TEOREMA DE BRIANCHON con el hexágono AC’BA’CB’ (en la figura vemos que las rectas que unen vértices opuestos concurren en un mismo punto O).