Propuesto por José María Pedret, ingeniero naval
Problema 216.- Dados dos triángulos homológicos, los puntos de intersección de los lados no homólogos están sobre una misma cónica
Pedret, J.M. (2005). Comunicación personal
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca (13 de febrero de 2005)Es una aplicación inmediata del recíproco del teorema de Pascal.
La condición necesaria y suficiente para que un hexágono esté inscrito en una cónica es que estén alineados los puntos de corte de los pares de lados opuestos.
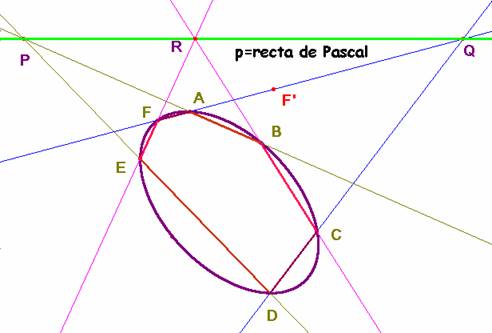
Para el teorema directo basta definir sobre la cónica la homografía (AEC) à (DBF). La recta de Pascal es el eje proyectivo de la misma.
Recíprocamente, si el hexágono ABCDE es tal que ABÇDE, BCÇEF y CDÇAF están alineados, los puntos A, B, C, D y E determinan una cónica única G. Esta cónica corta a la recta AF en un punto F’.
Aplicando el teorema directo al hexágono ABCDEF’ tenemos que ABÇDE, BCÇEF’ y CDÇAF’ están alineados, pero como las rectas AF y AF’ son iguales, esta recta coincide con la recta de Pascal de
ABCDEF pues ambas tienen iguales los puntos primero y tercero de los que sirven para definirlas.
Las rectas EF y EF’ cortan ambas a BC en el mismo punto R, por tanto F=F’ y los seis vértices del hexágono yacen sobre la cónica G.

En la figura tenemos los triángulos homológicos y los puntos de corte de los lados no homólogos, que etiquetamos con números del 1 al 6.
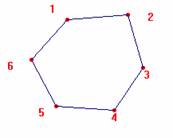 Observando estos puntos vemos que elegidos de forma adecuada dos a dos, las rectas que forman son los seis lados de los triángulos de partida, que por ser homológicos se cortan en puntos P, Q y R del eje de homología.
Observando estos puntos vemos que elegidos de forma adecuada dos a dos, las rectas que forman son los seis lados de los triángulos de partida, que por ser homológicos se cortan en puntos P, Q y R del eje de homología.
Solo hay que tomar una ordenación adecuada de ellos para formar un hexágono, cuya recta de Pascal sea el eje de homología. En el hexágono ─convexo o no─ de vértices 123456 son opuestos los lados 12 y 45, 23 y 56, 34 y 61. En nuestro caso 12=AB; 45=A’B’; 23=B’C’; 56 =BC; 34=AC y por último 61 =A’C’. El recíproco del teorema de Pascal nos asegura que los seis puntos yacen en una cónica. c.q.d.