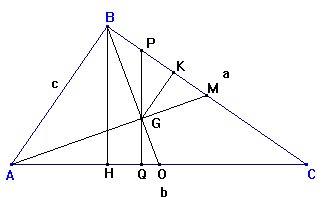
No es difícil hallar explícitamente PG y GQ:
Problema 217 de triánguloscabri |
|
|
|
Rodríguez, W. (2005): Comunicación personal.
|
Solución de Francisco Javier García Capitán

No es difícil hallar explícitamente PG y GQ: