Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú.

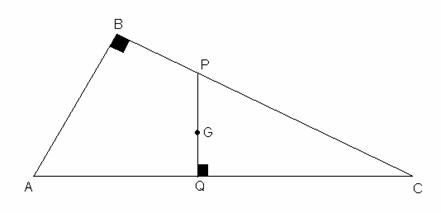
Problema 217  Si ABC es rectángulo y “G” su baricentro calcular la relación

Rodríguez, W. (2005): Comunicación personal.

Solución de Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid) :

Demos coordenadas a los puntos, sea B el (0,0), A el (a,0) y C el (0,c), luego G es el punto (a/3, c/3), y la recta AC es igual a AC: cx+a(y-c)=0.

La recta PQ será por tanto a(x-a/3)-c(y-c/3)=0, cortándolo con la recta BC: y=0 y AC obtenemos las coordenadas de los puntos P y Q.

P:((a²-c²)/3a,0) y Q:(a/3(2-a²/3(a²-c²)), c/3(1+a²/(a²+c²)).

Y entonces obtenemos que suponiendo que c>=a, PG/GQ=[(c²+a²)²/a⁴]^½ = b²/a²

Para el caso particular en que a=c, PG/GC=2.