|
DESARGUES Y PAPPUS
|
|
|
|
PROBLEMA 218 (15 de febrero de 2005 )
Sea ABC un triángulo, Por el pie A' de la altura por A, se trazan las perpendiculares a los lados AB y CA que cortan a las perpendiculares a BC desde B Y C en P y Q. Demostrar que los puntos P y Q están alineados con el ortocentro H del triángulo ABC. Jean-Claude Sidler. Géométrie projective 2e Édition. Dunod. Paris (2000); EXERCICES 2.4
La intención de este documento es descubrir a las HOMOGRAFÍAS y a la RAZÓN DOBLE como herramientas* para estudiar las figuras geométricas. El caso más simple es el de las homografías entre rectas proyectivas. Con el estudio de un tipo particular de homografías, que son las PROYECCIONES, se establecen dos resultados fundamentales de la geometría plana. El TEOREMA DE DESARGUES y el TEOREMA DE PAPPUS.
(*) Una vez establecidos los dos teoremas anteriores, los usamos par resolver varios ejercicios, entre ellos el problema propuesto
José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona). |
|
|
|
|
|
|
|
0. TEOREMAS PREVIOS |
|
|
|
Damos a continuación tres teoremas, que nos ayudan a establecer los resultados buscados. Para la demostración podemos consultar Jean-Claude Sidler. Géométrie projective 2e Édition. Dunod. Paris (2000) |
|
|
|
TEOREMA 0.1 ( HOMOGRAFIAS Y REFERENCIAS PROYECTIVAS ) Sean X0, X1... Xn+1 y X0’, X1’... Xn+1’ referencias proyectivas de P(E) y de P(E’) (espacios proyectivos). Existe entonces una homografía h y sólo una de P(E) sobre P(E’) tal que h(Xi)= Xi’ para i = 0...n+1. TEOREMA 0.2 ( HOMOGRAFIAS Y RAZON DOBLE ) Una homografía conserva la razón doble. Más precisamente, si h:X→h(X) es una homografía de P(E) sobre P(E’), para cuatro puntos cualesquiera, distintos y alineados X1, X2, X3, X4, los puntos h(X1), h(X2), h(X3), h(X4) están alineados, son distintos y cumplen la igualdad de razones dobles
( h(X1),h(X2),h(X3),h(X4) ) = ( X1,X2,X3,X4 ) *También es fácil calcular que
( A,B,C,X ) = ( A,B,C,Z ) ⇒ X = Z. TEOREMA 0.3 ( RAZON DOBLE DE PUNTOS Y RECTAS ) En un plano proyectivo. Sean a, b, c, d cuatro rectas distintas que pasan por un punto O. Una secante s que no pasa por O corta a estas cuatro rectas en los puntos A, B, C, D. Las razones dobles de las rectas y de los puntos son iguales
( a,b,c,d ) = ( A,B,C,D ) |
|
|
|
|
|
1. HOMOGRAFIAS ENTRE RECTAS PROYECTIVAS |
|
|
|
Un sistema de referencia de una recta proyectiva está constituido por tres puntos distintos. En estas condiciones el TEOREMA 0.1 adaptado a la recta proyectiva queda como |
|
|
|
TEOREMA 1.1 Sean A, B, C tres puntos distintos de una recta proyectiva r y A’, B’, C’ tres puntos distintos de una recta proyectiva r’. Existe entonces una homografía y sólo una
h: r → r’ tal que h(A) = A’, h(B) = B’, h(C) = C’. COROLARIO 1.1 Dos homografías entre rectas proyectivas que coinciden en tres puntos distintos son iguales. |
|
|
|
Podemos también adaptar un recíproco del TEOREMA 0.2 para homografías entre rectas proyectivas |
|
|
|
TEOREMA 1.2 Una biyección h:r→r’ entre dos rectas proyectivas es una homografía si y sólo si conserva la razón doble de cuatro puntos cualesquiera. DEMOSTRACION 1.2 Hemos destacado en el TEOREMA 0.2 que una homografía conserva la razón doble. Recíprocamente, sean A, B, C tres puntos distintos de r y A’, B’, C’ sus imágenes en r’ por la biyección h. Por el TEOREMA 1.1 existe una homografía g:r→r’ que transforma A en A’, B en B’, C en C’. Como g conserva la razón doble, para todo punto X de la recta r y distinto de A, B, C se tiene
( A,B,C,X ) = ( A’, B’,C’,h(X) ) = (A’,B’,C’,g(X) ) de donde (TEOREMA 0.2 *)
h(X) = g(X). |
|
|
|
Para obtener herramientas para resolver problemas, escribimos el TEOREMA 1.2 del siguiente modo |
|
|
|
TEOREMA 1.3 Una homografía h:r→r’ entre rectas, definida por las condiciones A→A’, B→B’, C→C’, transforma el punto X de r en un punto Z de r’ si y sólo si se cumple la relación
( A,B,C,X ) = ( A’,B’,C’,Z ). |
|
|
|
|
|
2. PROYECCIONES |
|
|
|
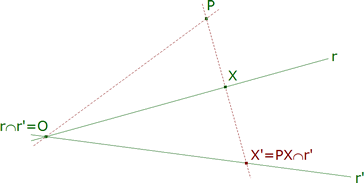
DEFINICION 2.1 (figura 1) En un plano proyectivo, sean r, r’ dos rectas proyectivas distintas y P un punto de dicho plano que no pertenece ni a r ni a r’. La aplicación de r sobre r’ que al punto X de r asocia el punto
X’ = PX ∩ r’ recibe el nombre de PROYECCION de centro P de r sobre r’. Esta aplicación es evidentemente una biyección; conserva la razón doble en virtud del TEOREMA 0.3. Y de acuerdo con el TEOREMA 1.2, es una homografía. |
|
|
|
Una proyección es una homografía. Veamos ahora como identificar de forma fácil una proyección. |
|
|
|
figura 1
TEOREMA 2.2 Una homografía entre dos rectas distintas de un plano proyectivo es una proyección si y sólo si el punto de intersección de estas rectas se transforma en sí mismo. DEMOSTRACION 2.2 directo (figura 1) Sea π: r → r’ una proyección. Pongamos O = r ∩ r’. Aplicando la DEFINICION 2.1 tenemos que π(O) = O. recíproco Sea h: r → r’ una homografía tal que h(O) = O. Consideremos dos puntos distintos A, B de r y distintos del punto O; gracias a esta elección, sus imágenes A’, B’ son distintas de A, B. Pongamos P = AA’ ∩ BB’ y tomemos la proyección π: r → r’ de centro P. Tenemos
π(A) = A’, π(B) = B’, π(O) = O. Las homografías h y π son iguales ya que coinciden en tres puntos distintos (COROLARIO 1.1) |
|
|
|
|
|
3. PRIMER TEOREMA DE DESARGUES |
|
|
|
Con un manejo genial de las proyecciones y del TEOREMA 2.2 aparece de forma sencilla el siguiente |
|
|
|
TEOREMA 3.1 ( PRIMER TEOREMA DE DESARGUES ) Sean ABC y A’B’C’ dos triángulos con vértices y lados distintos. Las intersecciones de los lados tomados dos a dos, es decir los puntos
P = AB ∩ A’B’, Q = BC ∩ B’C’, R = CA ∩ C’A’ están alineados si y sólo si las rectas
AA’, BB’, CC’ son concurrentes.
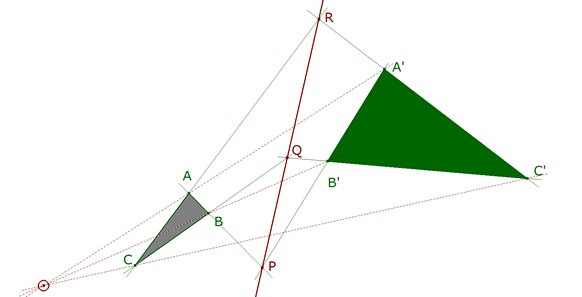
figura 2 DEMOSTRACION 3.1 directo Si las rectas AA’, BB’ y CC’ son concurrentes (figura 2), el TEOREMA 2.2 muestra que la homografía π: AA’ → CC’, compuesta con la proyección π1: AA’ → BB’ desde P y la proyección π2: BB’ → CC’ a partir de Q es también una proyección. De C = π(A) y C’ = π(A’), se deduce que R = AC ∩ A’C’ es el centro de π. Por construcción, los puntos X0 = PQ ∩ AA’ y π(X0) pertenecen a la recta PQ; como la recta X0π(X0) pasa por R, el punto R pertenece a la recta PQ. recíproco No es más que el dual. |
|
|
|
|
|
4. DESCOMPOSICION DE UNA HOMOGRAFIA |
|
|
|
Vamos a ver un teorema que nos permitirá descomponer una homografía en producto de dos proyecciones y con ello, la construcción geométrica de la imagen de un punto dado. |
|
|
|
TEOREMA 4.1 ( EJE DE HOMOGRAFIA ) Sea X→X’ una homografía h: r → r’ entre dos rectas proyectivas distintas. (1) Si h es una proyección, para todo par (X,Y) de puntos distintos de r, las rectas XY’ y YX’ se cortan sobre una recta fija que pasa por r ∩ r’. (2) Si h no es una proyección, para todo par (X,Y) de puntos distintos de r, las rectas XY’ y YX’ se cortan sobre la recta que une los puntos h(r∩r’) y h-1(r∩r’) La recta de los apartados (1) o (2) se denomina EJE DE LA HOMOGRAFIA. DEMOSTRACION 4.1
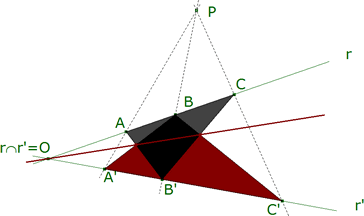
figura 3 parte (1) (figura 3) Se trata de un caso particular del PRIMER TEOREMA DE DESARGUES. Para convencerse de ello, basta con considerar tres puntos A, B, C y sus imágenes A’, B’, C’ por la proyección π:r→r’; y consideramos ahora los triángulos AB’C y A’BC’.
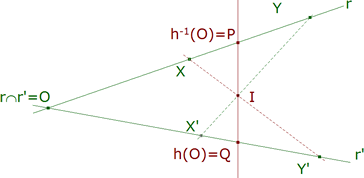
figura 4 parte (2) (figura 4) Pongamos O = r ∩ r’. Si h no es una proyección, los puntos P = h-1(O) y Q = h(O) son distintos de O de acuerdo con el TEOREMA 2.2. Sea X un punto de r distinto de O y de P. Consideremos ahora, la proyección π1: r → PQ de centro X’ = h(X) y la proyección π2: PQ → r’ de centro X. Las homografías h y π2ºπ1 coinciden sobre O, P, X, de acuerdo con el COROLARIO 1.1 son iguales. Aplicando sucesivamente π1 y π2 a un punto Y cualquiera de r diferente de O y de X, se construye Y’ y hemos demostrado el teorema. COROLARIO 4.1 De acuerdo con lo visto en la DEMOSTRACION 4.1, una homografía es, de un infinidad de maneras, un producto de dos proyecciones. |
|
|
|
|
|
5. TEOREMA DE PAPPUS |
|
|
|
5.1 CONSTRUCCION DEL EJE DE UNA HOMOGRAFIA ENTRE RECTAS PROYECTIVAS Sea X→X’ una homografía definida por las condiciones
A→A’, B→B’, C→C’. Se determina el eje de esta homografía construyendo los puntos
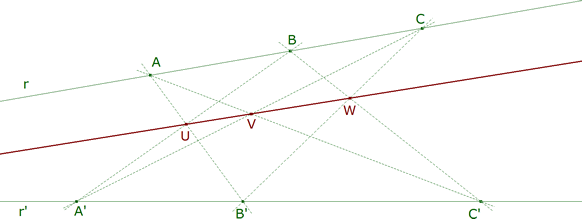
U = AB’ ∩ A’B y V = AC’ ∩ A’C (figura 4) De acuerdo con el TEOREMA 4.1, el punto W = BC’ ∩ B’C está alineado con los puntos U, V y esto no es más que el TEOREMA DE PAPPUS que se enuncia así |
|
|
|
TEOREMA 5.2 ( TEOREMA DE PAPPUS )
figura 5 Sean r, r’ dos rectas distintas y A, B, C tres puntos distintos de r y A’, B’, C’ tres puntos distintos de r’. Los puntos
U = AB’ ∩ A’B, V = AC’ ∩ A’C, W = BC’ ∩ B’C están alineados. |
|
|
|
|
|
6. TEOREMAS DUALES |
|
|
|
TEOREMA 6.1 ( DUAL DEL PRIMER TEOREMA DE DESARGUES ) Sean dos triángulos formados respectivamente por las rectas a, b, c y a’, b’, c’; si los puntos
a ∩ a’, b ∩ b’, c ∩ c’ son tres puntos alineados, entonces las rectas que unen los vértices
b ∩ c , b’ ∩ c’ c ∩ a , c’ ∩ a’ a ∩ b , a’ ∩ b’ son concurrentes.(misma figura 2) |
|
|
|
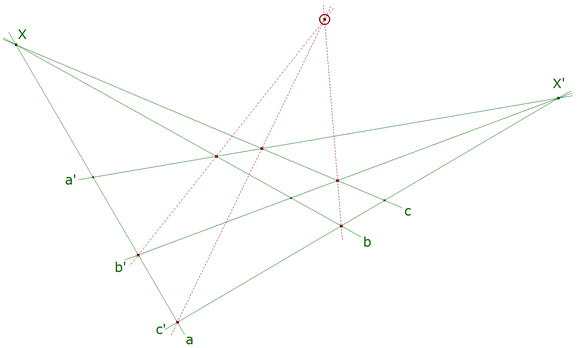
TEOREMA 6.2 ( DUAL DEL TEOREMA DE PAPPUS )
Sean tres rectas distintas a, b, c que pasan por un punto X y a’, b’, c’ tres rectas por un punto X’. Las rectas que unen los puntos
a ∩ b’ , a’ ∩ b b ∩ c’ , b’ ∩ c c ∩ a’ , c’ ∩ a son tres rectas concurrentes. |
|
|
|
|
|
7. APLICACION A LA SOLUCION DEL PROBLEMA 218 |
|
|
|
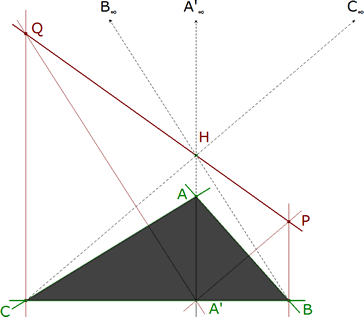
7.1 PROBLEMA 218 Sea ABC un triángulo, Por el pie A' de la altura por A, se trazan las perpendiculares a los lados AB y CA que cortan a las perpendiculares a BC desde B Y C en P y Q. Demostrar que los puntos P y Q están alineados con el ortocentro H del triángulo ABC.
figura 7 Dibujemos las tres alturas del triángulo dado. La perpendicular por B tiene la dirección B∞, es decir corta a la recta del infinito en B∞. La perpendicular por A’ tiene la dirección A’∞, es decir corta a la recta del infinito en A’∞. La perpendicular por C tiene la dirección C∞, es decir corta a la recta del infinito en C∞. Consideremos los puntos C, A’, B sobre la recta BC. Consideremos los puntos B∞, A’∞, C∞ sobre la recta del infinito. Q está sobre una paralela a CA’∞ y sobre una paralela a A’B∞ ⇒ Q = CA’∞ ∩ A’B∞. H está sobre una paralela a CC∞ y sobre una paralela a BB∞ ⇒ H = CC∞ ∩ BB∞. P está sobre una paralela a A’C∞ y sobre una paralela a BA’∞ ⇒ P = A’C∞ ∩ BA’∞. Entonces el TEOREMA DE PAPPUS (5.2) demuestra que Q, H, P están alineados.
|