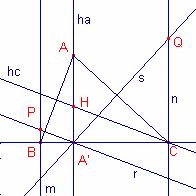
Siga el triangle .

Pel peu A’ de l’altura per A, es tracen les perpenciculars als costats i que tallen les perpenciulars a des de B i C respectivament en P i Q.

Demostreu que els punts P i Q estan alineats amb l’ortocentre H del triangle .

Solució Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):

Siga el triangle amb les coordenades cartesianes següents:

.

La recta altura al costat a té per equació: .

El peu de l’altura és .

La recta altura al costat c té per equació:

L’ortocentre és la intersecció de les dues rectes altures:

la solució del qual dóna el punt .

La recta perpendicular al costat que passa per A’ té per equació:

La recta perpendicular al costat que passa per B té per equació:

El punt P és la intersecció de les rectes r, m:

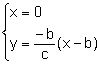la solució del qual dóna el punt .

La recta perpendicular al costat que passa per A’ té per equació:

La recta perpendicular al costat que passa per C té per equació:

El punt Q és la intersecció de les rectes s, n:

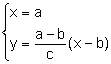la solució del qual dóna el punt .

Per veure que P, Q i H estan alineats comprovarem que els vectors són linealment dependents.

,

Vegem que les components són proporcionals:

.

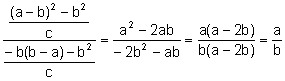Aleshores els punts P, Q, H estan alineats.