Problema 218
Sea ABC un triángulo.
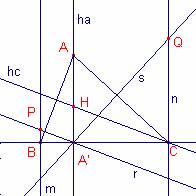
Por el pie A' de la altura por A, se trazan las
perpendiculares a los lados AB y CA que cortan a las perpendiculares a BC desde
B y C en P y Q.
Demostrar que los puntos P y Q están alineados con el ortocentro H del triángulo ABC.
Sidler, JC
(2000): Geometrie projective
2ª Edition. Dunod. Paris
Solución:
Sea el triángulo 
con las coordenadas
cartesianas siguientes:
.
La recta altura al lado a tiene por ecuación: 
.
El pie de la altura es 
.
La recta altura al lado c tiene por ecuación: 
El ortocentro es la intersección
de las dos rectas alturas:
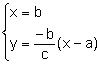la solución da el punto
.
La recta perpendicular al lado 
que pasa por A’ tiene
por ecuación:
La recta perpendicular al lado 
que pasa por B tiene por
ecuación:
El punto P es la intersección de las rectas r, m:
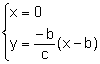la solución da el punto
.
La recta perpendicular al lado 
que pasa por A’ tiene
por ecuación:
La recta perpendicular al lado que pasa por C tiene por
ecuación:
El punto Q es la intersección de las rectas s, n:
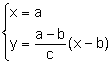la solución da el punto
.
Para ver que P, Q i H están alineados comprobaremos que los
vectores 
son linealmente dependientes.
, 
Veamos que las componentes son proporcionales:
.
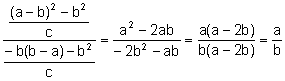Entonces los puntos P, Q, H están alineados.