Propuesto por José
María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)
Problema
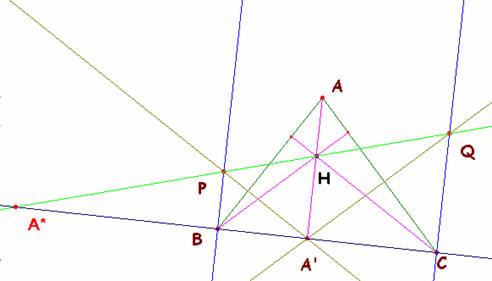
218.- Sea ABC un triángulo.
Por el pie A' de la altura por A, se trazan las perpendiculares a los lados AB
y CA que cortan a las perpendiculares a BC desde B y C en P y Q.
Demostrar que
los puntos P y Q están alineados con el ortocentro H del triángulo ABC. Sidler, JC (2000):
Geometrie projective 2ª Edition. Dunod.
Paris.
Solución del profesor Saturnino
Campo Ruiz, del IES Fray Luis de León de Salamanca.-
La situación
que nos presenta este problema es un caso particular de la que vamos a ofrecer
a continuación:

Supongamos un
triángulo ABC, una transversal r y tres rectas a, b y c
que pasando por los vértices de igual nombre concurren en un punto R de r. A’ es el punto de corte de la recta a
con el lado BC.
Dado el punto Y de b le hago
corresponder el punto X de a
y el punto Y’ de c según el método descrito en el dibujo. A saber:
- Proyección
de Y desde A’ sobre r en
el punto Z.
- Proyección
de Z desde C sobre la recta a en el punto X.
- Proyección
de X desde B sobre la recta r en el punto Z’,
y, finalmente
- Proyección
de Z’ desde A’ sobre c en el punto Y’.
Esta correspondencia (que evidentemente es proyectiva)
entre estas rectas puede hacerse indistintamente comenzando en cualquiera de
ellas a, b o c y
obteniendo siempre los mismo puntos. En particular, si se toma Y=B se
obtienen X=A’ e Y’=C.
Pues bien vamos a demostrar que los
puntos Y, X e Y’ están siempre alineados.
Sean A*, Y* los puntos de
intersección de la recta YX con las rectas BC y RC
respectivamente. Queremos concluir que Y*=Y’.
Los triángulos CY*X y A’XY son homológicos; el eje de
homología es r y el centro A*. En esta homología la imagen de la
recta A’X (que corta el eje en R) es la
recta YR=b y por ello la imagen
de A’ es el punto B, es
decir, que también son homológicos los triángulos A’Y*X y BXY de donde resulta que
los lados correspondientes A’Y* y BX cortan al eje r en el
punto Z y por tanto Y*=Y’como deseábamos.
Además, todas las ternas de puntos (Y,
X, Y’) están alineadas con A*. [1]
Para el caso del enunciado, la recta r es la
recta del infinito del plano. Las rectas b y c son las paralelas
a la altura a (=perpendiculares a BC por B y por C),
concurrentes en el punto del infinito R.
Si se elige X=H el ortocentro, los puntos correspondientes son P=Y,
Q=Y’, que están alineados con A*.