Enunciado del problema

Una recta d corta los lados AB, BC, CA de un triángulo ABC en C', A', B' respectivamente. Sean L la intersección de AA' con BB', M la intersección de BB' con CC' y N la intersección de CC' con AA'. Demostrar que las rectas AM, BN y CL son concurrentes.

Cell[GraphicsData[Bitmap, CF5dJ6E]HGAYHf4PAg9QL6QYHg<PAVmbKF5d0`40009D0001>2000`400?l0<b ... geSize -> {596., 312.}, ImageMargins -> {{0., 0.}, {0., 0.}}, ImageRegion -> {{0., 1.}, {0., 1.}}]

Fórmulas necesarias

Como estamos usando Mathematica para resolver el problema, representamos puntos y rectas como ternas {u,v,w} de números.

Usaremos la misma función Unir para hallar el punto de intersección de dos rectas y para hallar la recta que une dos puntos.

 

Unir[{x1_, y1_, z1_}, {x2_, y2_, z2_}] :=  {Det[(y1 z1)], -Det[(x1 z1)], Det[(x1 ... y2 z2 x2 z2 x2 y2

Introducción de datos

Ahora  introducimos directamente las coordenadas de algunos de los puntos que intervienen en el problema:

 

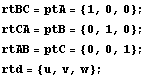
rtBC = ptA = {1, 0, 0} ; rtCA = ptB = {0, 1, 0} ; rtAB = ptC = {0, 0, 1} ; rtd = {u, v, w} ;

Cálculos

Vamos haciendo los cálculos especificados por el enunciado:

 

ptA1 = Unir[rtd, rtBC] ptB1 = Unir[rtd, rtCA] ptC1 = Unir[rtd, rtAB]

{0, w, -v}
{-w, 0, u}
{v, -u, 0}

 

ptL = Unir[Unir[ptA, ptA1], Unir[ptB, ptB1]] ptM = Unir[Unir[ptB, ptB1], Unir[ptC, ptC1]] ptN = Unir[Unir[ptC, ptC1], Unir[ptA, ptA1]]

{v w, u w, -u v}
{-v w, u w, u v}
{v w, -u w, u v}

 

rtAM = Unir[ptA, ptM] rtBN = Unir[ptB, ptN] rtCL = Unir[ptC, ptL]

{0, -u v, u w}
{u v, 0, -v w}
{-u w, v w, 0}

 

Las tres rectas serán concurrentes si y solo si su determinante es cero:

Det[{rtAM, rtBN, rtCL}]

0

Created by Mathematica  (March 1, 2005)