|
DESARGUES
|
|
|
|
220 (1 de marzo de 2005) Una recta d corta los lados AB, BC, CA de un triángulo ABC en C', A', B' respectivamente. Sean L=AA'∩BB', M=BB'∩CC' y N=CC'∩AA'. Demostrar que las rectas AM, BN y CL son concurrentes.
Solución de José María Pedret. Ingeniero Naval. Esplugues de Llobregat (Barcelona).
UNA VISIÓN MÁS EXHAUSTIVA DE LAS BASES TEÓRICAS QUE LLEVAN AL TEOREMA DE DESARGUES PUEDE ENCONTRARSE EN EL PROBLEMA 218
|
|
|
1. PRIMER TEOREMA DE DESARGUES |
|
|
|
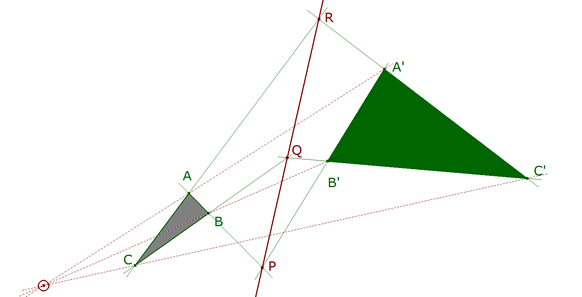
TEOREMA ( PRIMER TEOREMA DE DESARGUES ) Sean ABC y A’B’C’ dos triángulos con vértices y lados distintos. Las intersecciones de los lados tomados dos a dos, es decir los puntos
P = AB ∩ A’B’, Q = BC ∩ B’C’, R = CA ∩ C’A’ están alineados si y sólo si las rectas
AA’, BB’, CC’ son concurrentes.
figura 1 DEMOSTRACION 3.1 directo Si las rectas AA’, BB’ y CC’ son concurrentes (figura 1), la homografía π: AA’ → CC’, compuesta con la proyección π1: AA’ → BB’ desde P y la proyección π2: BB’ → CC’ a partir de Q es también una proyección. De C = π(A) y C’ = π(A’), se deduce que R = AC ∩ A’C’ es el centro de π. Por construcción, los puntos X0 = PQ ∩ AA’ y π(X0) pertenecen a la recta PQ; como la recta X0π(X0) pasa por R, el punto R pertenece a la recta PQ. recíproco No es más que el dual. |
|
|
|
2. TEOREMA DUAL |
|
|
|
TEOREMA ( DUAL DEL PRIMER TEOREMA DE DESARGUES ) Sean dos triángulos formados respectivamente por las rectas a, b, c y a’, b’, c’; si los puntos
a ∩ a’, b ∩ b’, c ∩ c’ son tres puntos alineados, entonces las rectas que unen los vértices
b ∩ c , b’ ∩ c’ c ∩ a , c’ ∩ a’ a ∩ b , a’ ∩ b’ son concurrentes.(misma figura 1) |
|
|
|
3. APLICACION |
|
|
|
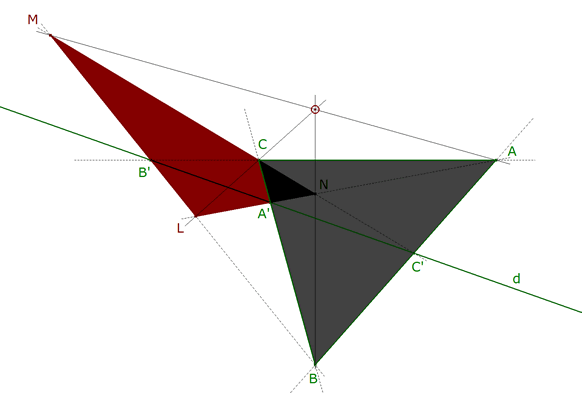
SOLUCION DEL PROBLEMA 220 Una recta d corta los lados AB, BC, CA de un triángulo ABC en C', A', B' respectivamente. Sean los puntos L = AA' ∩ BB', M = BB' ∩ CC' y N = CC' ∩ AA'. Demostrar que las rectas AM, BN y CL son concurrentes.
Dibujamos L, M, N. Lo primero que vemos es que los triángulos ABC y LMN son homológicos. Basta observar que
A’ = BC ∩ NL B’ = CA ∩ LM C’ = AB ∩ MN Entonces gracias al TEOREMA DE DESARGUES como A’, B’, C’ están alineados sobre la recta d entonces AM, BN, CL son concurrentes.
|