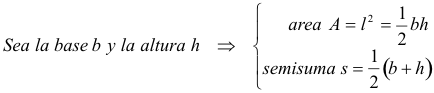
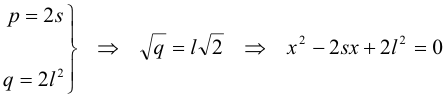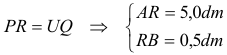Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid)

Para el aula

Problema 221

183. El área de un triángulo es 1,25dm cuadrados . La semisuma de un lado y su altura respectiva es 2,75 dm. Hallar el valor de dicha altura.

MATEMATICA ELEMENTAL (1947) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VII nº1

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat.

(1 de marzo de 2005)

Hagamos ahora un inciso para resolver la ecuación de segundo grado

Es decir, conocemos la suma y el producto de las raíces.

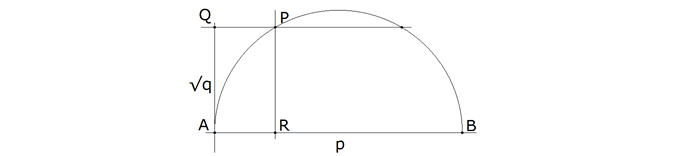
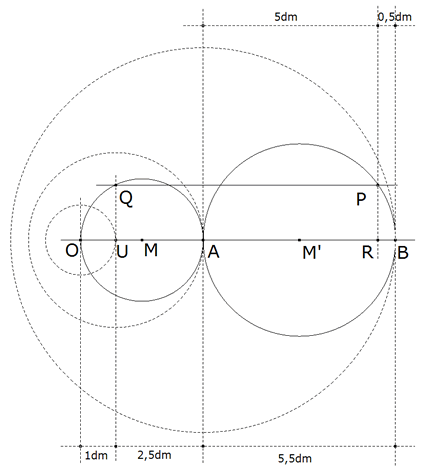
Figura 1

Trazamos un círculo de diámetro la suma p. Siendo el producto q, trazamos una paralela al diámetro distante √q, que cortará en P al semicírculo. Por P la perpendicular al diámetro lo corta en R que nos separa las raíces

En nuestro problema, la ecuación es:

Hemos obtenido la construcción general para determinar h. En este caso particular sustituyendo valores numéricos

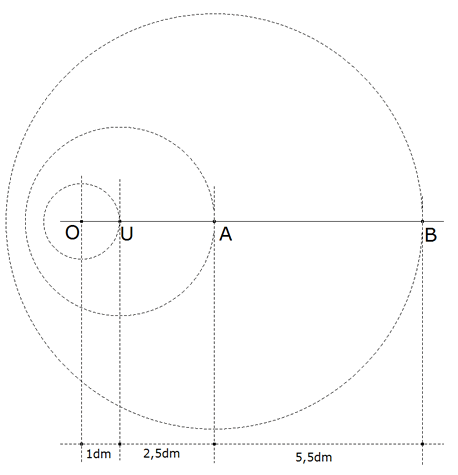
Figura 2

Trazamos la unidad OU, UA=2,5. AB=5,5

Figura 3

Sea M punto medio de OA

y además M’ es el punto medio de AB

que son las soluciones buscadas