Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid)

Para el aula

Problema 221

183. El área de un triángulo es 1,25dm cuadrados . La semisuma de un lado y su altura respectiva es 2,75 dm. Hallar el valor de dicha altura.

MATEMATICA ELEMENTAL (1947) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VII nº1

Solución de Ricard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València) :

Sea el triángulo tal que: ,

Resolviendo el sistema formado por ambas ecuaciones:

las soluciones son:

, .

Construcción con regla y compás:

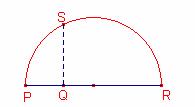
1.- Sea ,

2.- Dibujemos la semicircunferencia de diámetro .

3.- Tracemos una perpendicular al diámetro por el punto Q.

4.- Entonces .

5.- Sea .

6.- Dibujemos la semicircunferencia de diámetro .

7.- Tracemos la perpendicular al diámetro por el punto T.

8.- Sea .

9.- Tracemos la paralela al diámetro que pasa por el punto X que corta la semicircunferencia en el punto Z.

10.- Tracemos la perpendicular al diámetro por el punto Z que corta el diámetro en el punto Y.

11.- Entonces la altura es o .

Applet created on 1/03/05 by Ricard Peiró with CabriJava