Propuesto por Ricard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València)
Problema 222
En la
hipotenusa de un triángulo rectángulo, como sobre un lado, se ha construido un
cuadrado (fuera del triángulo). El centro del cuadrado está unido con el
vértice del ángulo recto del triángulo. ¿En qué segmentos se divide la
hipotenusa si los catetos son iguales a 21 y
Gúsiev , V.y
otros (1989) "Prácticas para resolver Problemas matemáticos.
Geometría" Ed . Mir . Problema 185 pàgina 47
Solución de Profesor Julio Miranda Ubaldo (Huaral – Perú)
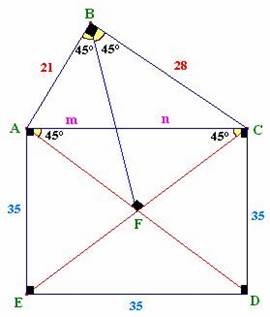
Por el T de Pitágoras la hipotenusa AC mide 35.
Es decir de la figura : m + n = 35 .....(1)
Sabemos que el centro del cuadrado F es el punto de corte de sus diagonales ,
dichas diagonales se cortan perpendicularmente y
son a su vez bisectrices de los ángulos rectos del cuadrado.
De otro lado el cuadrilátero ABCF es inscriptible entonces:
m<ABF = m<AFC = 45°, y m<FBC = m<FAC = 45°,
se demuestra entonces que BF es bisectriz del ángulo recto B.
Por el Teorema de
Relacionando (1) y (2) tendremos que :
m = 15 y n = 20.