Problema 222

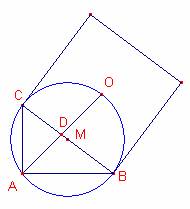
En la hipotenusa d’un triangle rectangle, com costat s’ha construït un quadrat exterior al triangle. El centre del quadrat està unit amb el vèrtex de l’angle recte del triangle. Amb quins segments ha quedat dividit la hipotenusa si els catets són iguals a 21 cm i 28 cm.

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Problema 185 pàgina 47

Solució 1:

Siga el triangle rectangle .

Aplicant el teorema de Pitàgores al triangle :

.

Siga M el punt mig de la hipotenusa, que és el centre de la circumferència circumscrita al triangle .

Siga O el centre del quadrat exterior al triangle dibuixat sobre la hipotenusa.

Siga D la intersecció dels segments .

Notem que l’arc mesura 90º, aleshores, per ser un angle inscrit en la circumferència.

Notem que per ser un angle interior a la circumferència i els arc mesuren , .

Aplicant el teorema dels sinus al triangle :

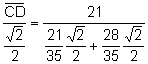, , simplificant:

.

.

Solució 2:

Aplicant el teorema de Pitàgores al triangle :

.

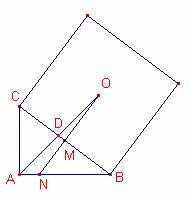
Siga N la intersecció de la recta OM i el costat .

Els triangles , són semblants, aplicant el teorema de Tales:

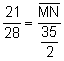, aleshores, . 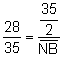, aleshores,

. .

Notem que .

Siga .

Aplicant el teorema dels sinus al triangle :

,

.

.

.

.

.

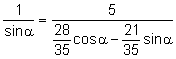Aplicant raons trigonomètriques al triangle rectangle :

, aleshores, .

.

.