Problema 222

Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

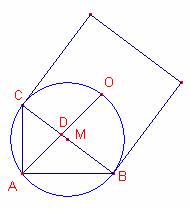
En la hipotenusa de un triángulo rectángulo, como sobre un lado, se ha construido un cuadrado (fuera del triángulo). El centro del cuadrado está unido con el vértice del ángulo recto del triángulo. ¿En qué segmentos se divide la hipotenusa si los catetos son iguales a 21 y 28 cm?

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Problema 185 página 47

Solución 1:

Sea el triángulo rectángulo .

Aplicando el teorema de Pitàgores al triángulo :

.

Sea M el punto medio de la hipotenusa, que es el centro de la circunferencia circunscrita al triángulo .

Sea O el centro del cuadrado exterior al triángulo dibujado sobre la hipotenusa.

Sea D la intersección de los segmentos .

Notemos que el arco mesura 90º, entonces, por ser un ángulo inscrito en la circunferencia.

Notemos que por ser un ángulo interior a la circunferencia y los arcos miden , .

Aplicando el teorema de los senos al triángulo :

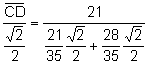, , simplificando:

.

.

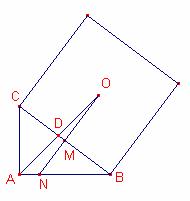
Solución 2:

Aplicando el teorema de Pitágoras al triángulo :

.

Sea N la intersección de la recta OM y el lado .

Los triángulos , son semejantes, aplicando el teorema de Tales:

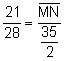, entonces, . 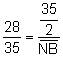, entonces,

. .

Notemos que .

Sea .

Aplicando el teorema de los senos al triángulo :

,

.

.

.

.

.

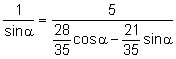Aplicando razones trigonométricas al triángulo rectángulo :

, entonces, .

.

.