Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 222.- En la hipotenusa de un triángulo rectángulo, como sobre un lado, se ha construido un cuadrado (fuera del triángulo). El centro del cuadrado está unido con el vértice del ángulo recto del triángulo. ¿En qué segmentos se divide la hipotenusa si los catetos son iguales a 21 y 28 cm?

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Problema 185 página 47.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca (2 de marzo de 2005)

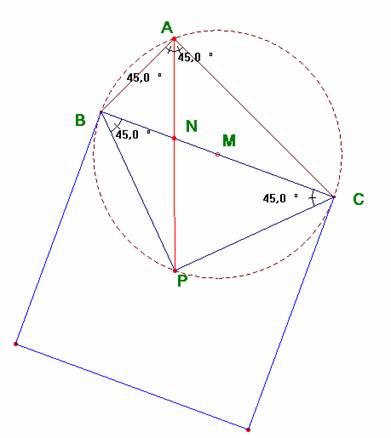
El cuadrilátero ABCP tiene igual a 90º los ángulos de los vértices A y P. Por tanto es inscriptible en una circunferencia. De ahí, con un simple cómputo de los ángulos inscritos, se deduce que AP es la bisectriz del ángulo recto. Los segmentos pedidos se calculan de inmediato.

Según el teorema de la bisectriz ; despejando BN =; CN =.

Si los catetos miden 21 y 28 cm, por el teorema de Pitágoras, la hipotenusa mide 35. Aplicando las expresiones anteriores resultan BN= 15; CN = 35-15 = 20.