Enunciado del problema

Consideremos un triángulo ABC cualquiera. Sean D y E puntos sobre el lado BC, F y G puntos sobre el lado CA yH y I puntos sobre el lado AB, tal que BD:DE:EC = CF:FG:GA = AH:HI:IB = p:q:r con p+q+r=1, p,q, r > 0.Sean K,L y M los puntos de intersección de las diagonales DG y EH, FI y DG, y EH y FI. Probar que :
- El área de los cuadriláteros DEFG, FGHI, y HIDE es igual a q veces el área de ABC.
- Las áreas de los triángulos GHK, IDL y EFM son iguales a k -se hallará- veces el área de ABC.
- Las áreas de los triángulos DEK, FGL y HIM son iguales a h -se hallará- veces el área de ABC
- El área del triángulo KLM es igial a l -se hallará-, veces al área de ABC.

Cell[GraphicsData[Bitmap, CF5dJ6E]HGAYHf4PAg9QL6QYHg<PAVmbKF5d0`40008k0001;a000`40O003<br / ... geSize -> {571., 303.}, ImageMargins -> {{0., 0.}, {0., 0.}}, ImageRegion -> {{0., 1.}, {0., 1.}}]

Fórmulas necesarias

Como estamos usando Mathematica para resolver el problema, representamos puntos y rectas como ternas {u,v,w} de números. Teniendo en cuenta que {au, av, aw} es equivalente a {u,v,w}, usaremos una función Simplificar para eliminar factores como el a anterior.

Simplificar[{x_, y_, z_}] := Factor[{x, y, z}/PolynomialGCD[x, y, z] ] ;

Usaremos también la misma función Unir para hallar el punto de intersección de dos rectas y para hallar la recta que une dos puntos.

Unir[{x1_, y1_, z1_}, {x2_, y2_, z2_}] := Simplificar[{Det[(y1 z1)], -Det[(x1 z1)] ... y2 z2 x2 z2 x2 y2

Finalmente, definimos las funciones que calculan el área de un triángulo y de un cuadrilátero en coordenadas baricéntricas.

AreaTriangulo[{x1_, y1_, z1_}, {x2_, y2_, z2_}, {x3_, y3_, z3_}] := Simplify[1/((x1 + ... x3 y3 z3

Introducción de datos

Ahora  introducimos directamente las coordenadas de algunos de los puntos que intervienen en el problema:

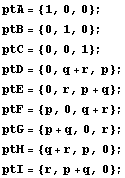
ptA = {1, 0, 0} ; ptB = {0, 1, 0} ; ptC = {0, 0, 1} ; ptD = {0, q + r, p} ; ptE = {0, r, p + q} ; ptF = {p, 0, q + r} ; ptG = {p + q, 0, r} ; ptH = {q + r, p, 0} ; ptI = {r, p + q, 0} ;

Usamos la función Unir para hallar los tres puntos de intersección de las diagonales

ptK = Unir[Unir[ptD, ptG], Unir[ptE, ptH]] ptL = Unir[Unir[ptF, ptI], Unir[ptD, ptG]] ptM = Unir[Unir[ptE, ptH], Unir[ptF, ptI]]

{q (p + q) (q + r), (q + r) (p^2 + p q - p r + r^2), (p + q) (p^2 - p r + q r + r^2)}

{-(p + q) (p^2 - p r + q r + r^2), -q (p + q) (q + r), -(q + r) (p^2 + p q - p r + r^2)}

{(q + r) (p^2 + p q - p r + r^2), (p + q) (p^2 - p r + q r + r^2), q (p + q) (q + r)}

Cálculos

Ahora, calculamos las áreas de todos los triángulos y cuadriláteros pedidas en el enunciado.

DEFG = AreaCuadrilatero[ptD, ptE, ptF, ptG]

q/(p + q + r)

FGHI = AreaCuadrilatero[ptF, ptG, ptH, ptI]

q/(p + q + r)

HIDE = AreaCuadrilatero[ptH, ptI, ptD, ptE]

q/(p + q + r)

GHK = Area[ptG, ptH, ptK]

(p^4 + p^3 (q - 2 r) + 3 p^2 r^2 + r^3 (q + r) + p r (q^2 - 2 r^2))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

IDL = Area[ptI, ptD, ptL]

(p^4 + p^3 (q - 2 r) + 3 p^2 r^2 + r^3 (q + r) + p r (q^2 - 2 r^2))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

EFM = Area[ptE, ptF, ptM]

(p^4 + p^3 (q - 2 r) + 3 p^2 r^2 + r^3 (q + r) + p r (q^2 - 2 r^2))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

DEK = Area[ptD, ptE, ptK]

(q^2 (p + q) (q + r))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

FGL = Area[ptF, ptG, ptL]

(q^2 (p + q) (q + r))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

HIM = Area[ptH, ptI, ptM]

(q^2 (p + q) (q + r))/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

KLM = Area[ptK, ptL, ptM]

(p^2 - q^2 - p r + r^2)^2/((p + q + r)^2 (p^2 + q^2 + p (q - r) + q r + r^2))

Created by Mathematica  (March 1, 2005)