Propuesto por William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú.

Problema 224

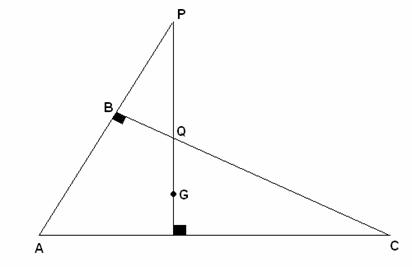
En la siguiente gráfica se cumple que: , y ABC es rectángulo si “G” su baricentro calcular el ángulo ACB

Rodríguez, W. (2005): Comunicación personal.

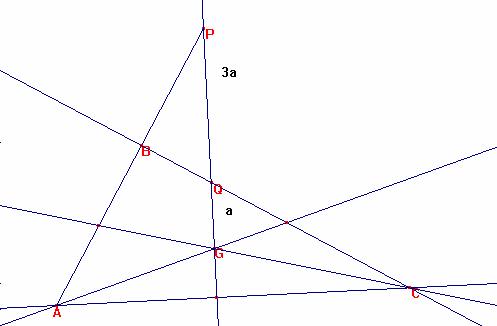
Solución del editor:

Supongamos que la figura cumple las condiciones del problema. Tracemos desde A1, punto medio de BC una semejanza del segmento QG de razón 3.

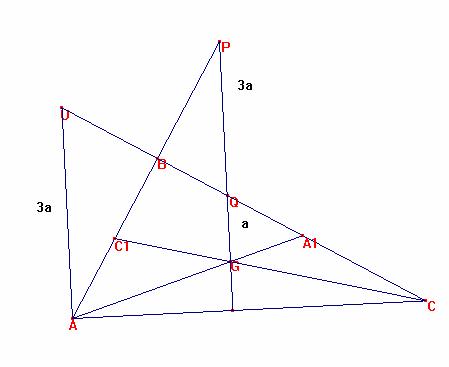
Los triángulos QPB y UAB son rectángulos en B, semejantes por tener <Q=<U, <A=<P, y con la hipotenusa igual a 3a, luego AB=BP, y IB=BQ = 2 AC1.

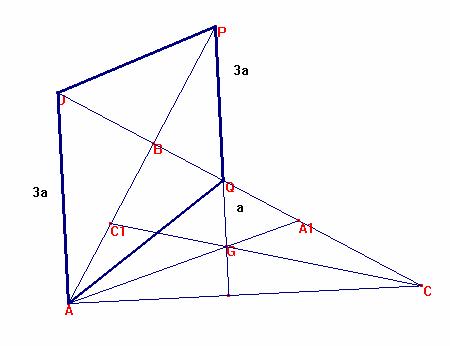
Luego AUPQ “debe” ser rombo (Como se ha hecho una “suposición” de cumplir las condiciones del enunciado, no lo es realmente).

Consideremos ahora la mediana B B1 de B en ABC.

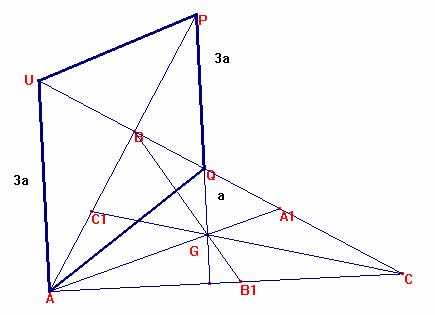
El triángulo BB1C es isósceles, y <QBG= <BCB1, por lo que los triángulos

BQG y PBG son semejantes al tener iguales los ángulos <BPG=<GBQ=GCb, del que se nos pide la medida y los <PGB= <BGQ por ser comunes.

Luego es PG / BG = GB/GQ = PB / BQ.

Es decir, GBGB = PG GQ = (4 a) a , y GB=2a.

Luego PB/BQ= 2 a /a = 2, y por ello, es BQ= PB/2 = AC1.

De esta manera, en el triángulo rectángulo PBQ es PB = 2AC1, BQ = AC1, PQ = 3a

Y es PB PB + BQ BQ = PQ PQ, luego es 4AC1 AC1 + AC1 AC1 = 9aa,

5 AC1 AC1 = 9aa, por lo que AC1 = (3 sqr (5)) a /5,

Y AP = 4 ( (3 sqr (5)) a /5) = (12 sqr (5) a )/5.

Ahora podemos construir la situación geométrica descrita:

Sea a un segmento.

Construyamos el triángulo rectángulo en B PBQ de hipotenusa QP= 3a y catetos

BQ= (3 sqr (5)) a /5, y PB= (6 sqr (5)) a /5.

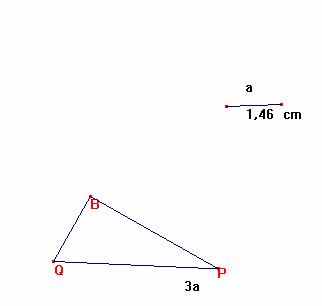
Continuemos la construcción:

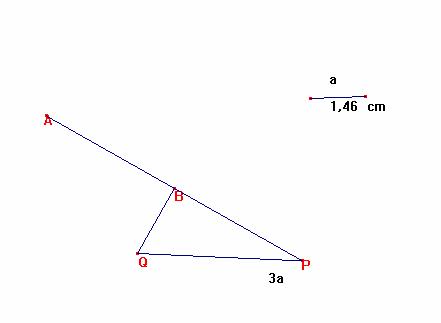
A es el simétrico de P respecto a B.

PQ forma con AC un ángulo recto, luego tracemos la circunferencia de diámetro PA:

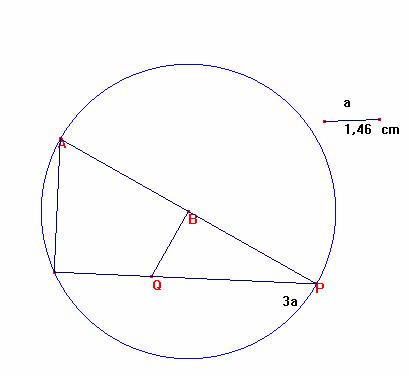
Prolonguemos BQ y el cateto desde A:

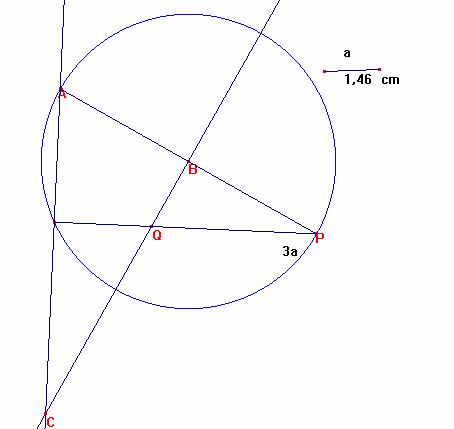
Tendremos la construcción completa de la figura.

Por último, hallemos el valor del ángulo pedido:

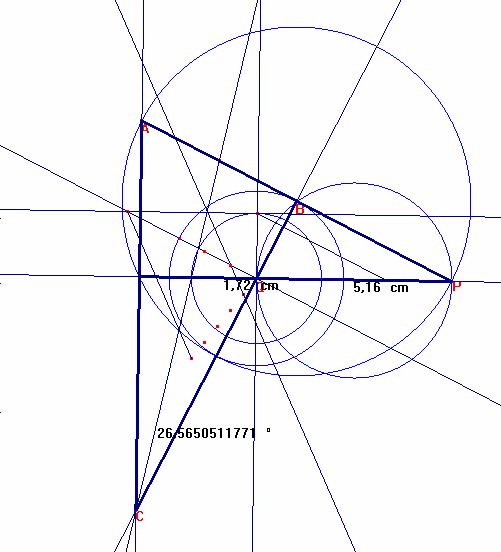
<C= <P= arctg ½= 26,57ª

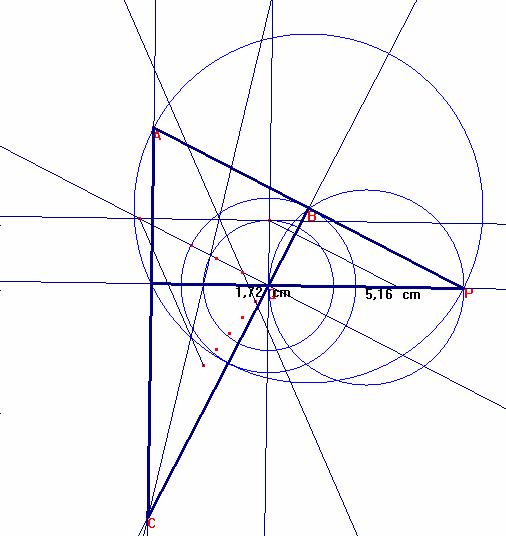
Ángulo en C:

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla