Para el aula
Propuesto por Maite Peña Alcaraz, estudiante de Industriales
en
Problema 226.1
212. Calcular el área de un triángulo isósceles inscrito en una circunferencia de radio 30 dm y base 10dm.
EJERCICIOS ELEMENTALES PROPUESTOS: (1948) MATEMATICA
ELEMENTAL ( 4ª Serie – Tomo
VIII nº1 ) Revista publicada por el instituto Jorge
Juan de matemáticas y
Soluciónes
de William Rodríguez Chamache, profesor de
Sea AB la base del triángulo inscrito en la circunferencia entonces la mediatriz de este lado pasa por el centro de la circunferencia que lo inscribe
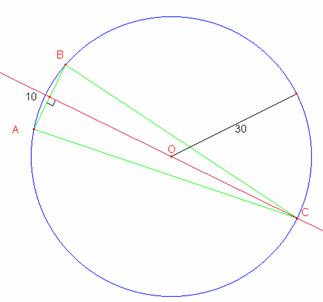
Ahora en el triángulo rectángulo BNO por Pitágoras obtenemos
el segmento NO=![]() =
=![]() =29,58
=29,58
Finalmente el área del triángulo será: ![]() = 297,90u2
= 297,90u2
Sea AB la base del triángulo inscrito en la circunferencia entonces la mediatriz de este lado pasa por el centro de la circunferencia que lo inscribe y corta al arco de circunferencia AB en Q siendo el triángulo AQB otra solución. Al problema
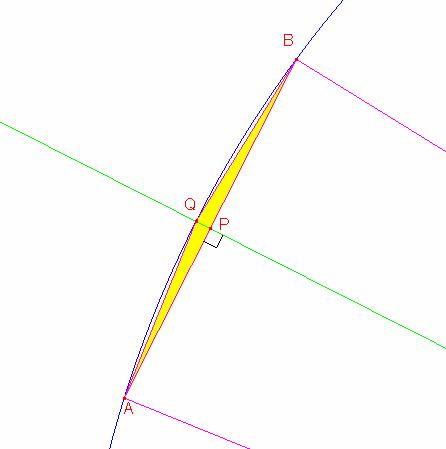
Ahora en el triángulo rectángulo BPO: por Pitágoras
obtenemos el segmento PO=![]() =
=![]() =29,58
=29,58
Pero en el triángulo rectángulo BQP: podemos calcular la
altura QP= ![]()
Finalmente el área del triángulo AQB=![]() dm2
dm2