Problema 227

416 Construir un triángulo rectángulo conociendo la hipotenusa y la bisectriz del ángulo recto.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución del editor.-

Se conocen 2a y m.

Hipotenusa 2 a y bisectriz m.

Sea p la continuación desde el pie de la bisectriz a la circunferencia

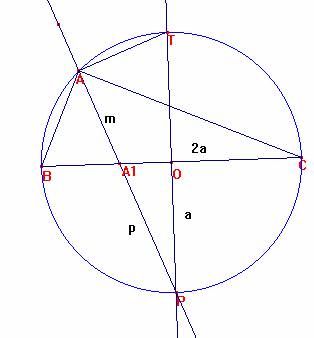
POA1 es semejante a PAT.

a/p = (m+p) / 2a

Luego es 2 a ² = m p + p ²

O sea: tenemos que es 2 a ² - m p - p ² =0, con a y m conocidos.

p ² + m p - 2 a ² =0

p = (- m + - ( sqr ( m ² + 8 a ² ))/2

y tenemos que

m+p = ( m + - ( sqr ( m ² + 8 a ² ))/2

Veamos la construcción de m+p. Tomemos el signo +

8 a ² = (sqr (2 ) 2 a )² que es el cuadrado de la diagonal del cuadrado de la hipotenusa.

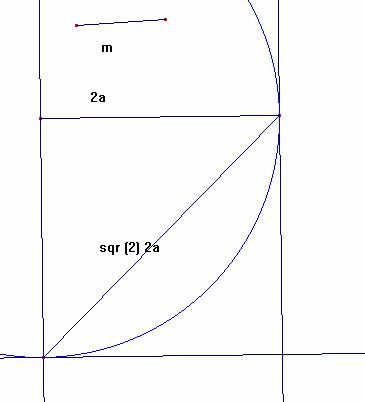
Ahora llevemos el segmento m perpendicularmente sobre un extremo de tal diagonal:

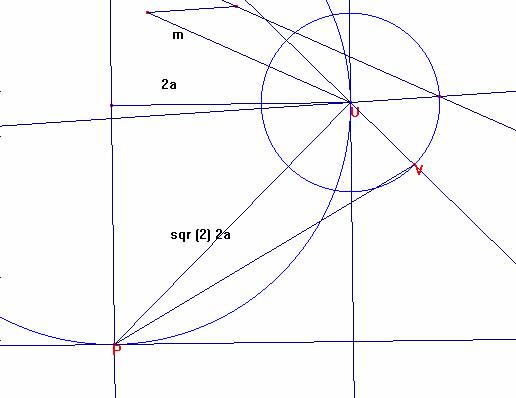
Por paralelas llevo m a U y por una circunferencia de centro U, y radio m y la perpendicular UV a PU, obtengo PV que es sqr ( m ² + 8 a ² ).

Sumamos m a PV:

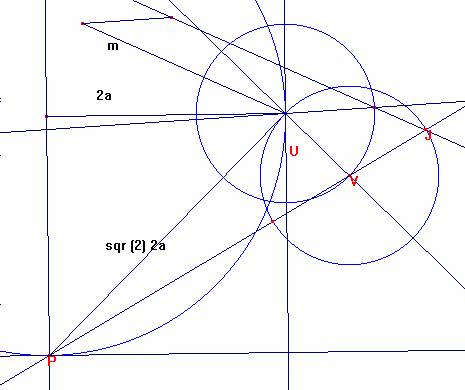
PJ es ( m + ( sqr ( m ² + 8 a ² ))

Tomando la mitad de PJ, tenemos :

PK= m+p = ( m + ( sqr ( m ² + 8 a ² ))/2

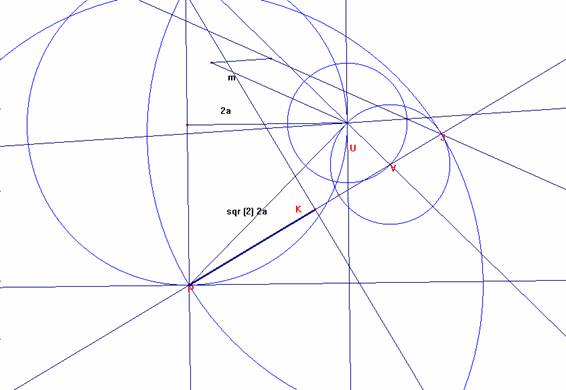
Los elementos esenciales son:

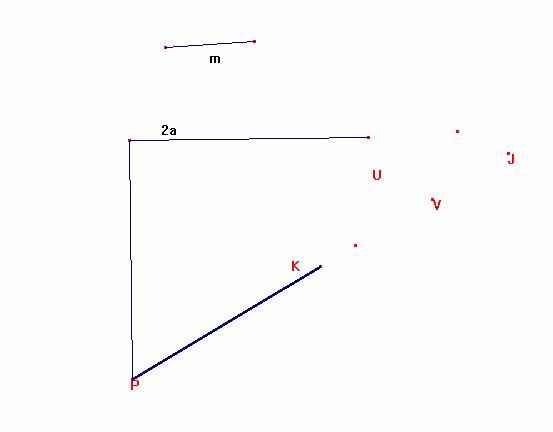
Trazamos ahora dos circunferencias:

La de diámetro 2 a (la vertical) y la de radio PK (p+m), y tenemos la solución:

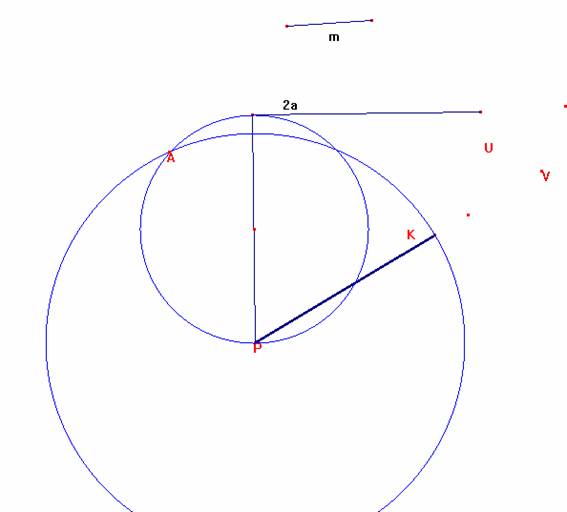
Ahora tracemos el diámetro perpendicular y obtenemos el triángulo pedido:

 Lógicamente 0<m<=a, es decir, la mitad de la hipotenusa es l mayor valor que puede tomar la bisectriz.

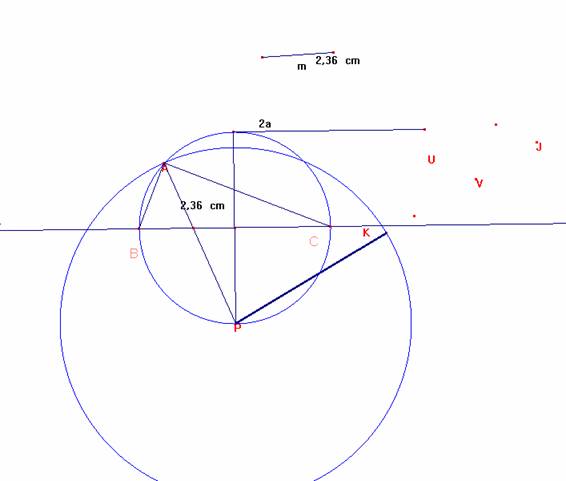
^{Ricardo Barroso Campos}

^{Didáctica de las Matemáticas}

^{Universidad de Sevilla}