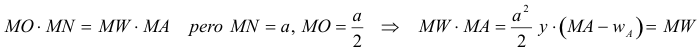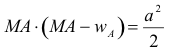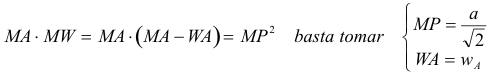Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat. (16 de marzo de 2005)

Teorema I ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 51)
En una misma circunferencia o en circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales, y a arcos iguales corresponden ángulos centrales iguales.

Teorema II ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 53)
El lugar geométrico de los vértices de todos los ángulos directamente congruentes entre sí cuyos lados pasan por dos puntos fijos A y B, es un arco de circunferencia de extremos A y B, llamado arco capaz del ángulo sobre el segmento AB.

Teorema III ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 84)
Todo ángulo inscrito en una circunferencia es igual a la mitad del central que comprende el mismo arco.

Teorema IV ( Es consecuencia de I, II y III)
La bisectriz del ángulo inscrito en una circunferencia pasa por el punto medio del arco capaz.

Teorema V ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 86)
En todo cuadrilátero inscriptible (convexo) los ángulos opuestos son suplementarios. Todo cuadrilátero que tiene dos ángulos opuestos suplementarios es inscriptible.

Teorema VI ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 135)
Si desde un punto del plano de una circunferencia se trazan secantes a la misma, el producto de distancias de dicho punto a los de intersección de cada secante es una constante.

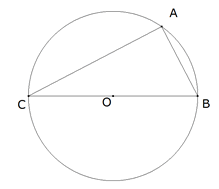
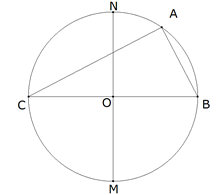
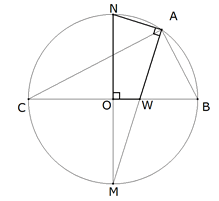
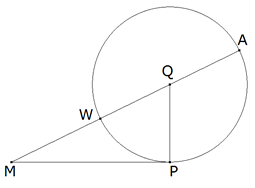
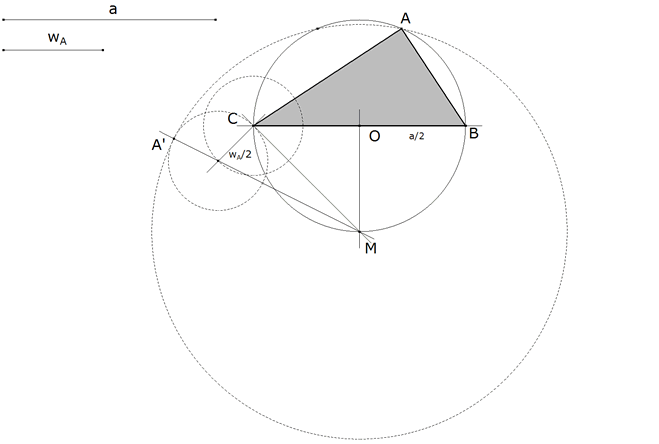
Supongamos el problema resuelto.


Figura 1

Si el arco es una semicircunferencia el ángulo central es π.

Si consideramos CAB inscrito en un círculo, como CAB=π/2, el valor del ángulo central es el doble BOC=π . (II y III)

Por lo tanto, podemos considerar al triángulo rectángulo como inscrito en un círculo cuyo diámetro es la hipotenusa y el vértice del ángulo recto sobre la circunferencia.

Figura 2

Trazamos MN el diámetro perpendicular a BC. MOB=π/2; pero como BOC=π entonces M es el punto medio del arco BMC. (III)

Figura 3

AM es la bisectriz y corta a BC en W;  (IV) ya que arco BM=arco MC entonces ángulo BAM=ángulo MAC

Figura 4

Como MN es un diámetro, AMN también es un triángulo rectángulo. (II y III)

Figura 5

Por lo visto hasta aquí, NOW=NAW=π/2; pero estos dos son ángulos opuestos del cuadrilátero AWON y como NOW+NAW=π, son suplementarios y por tanto AWON es un cuadrilátero inscriptible. (V)

Figura 6

Entonces A, W, O, N están sobre la misma circunferencia y entonces se cumple (VI)



que se traduce en la siguiente igualdad

Resolvamos ahora la igualdad anterior


Figura 7

Observando la figura 7 vemos que (VI)



MP es la diagonal de un cuadrado de lado a/2. Obtenida MA podemos trazar la solución.

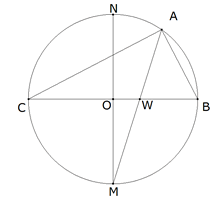
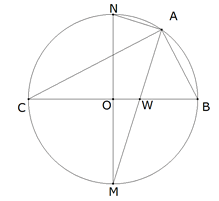
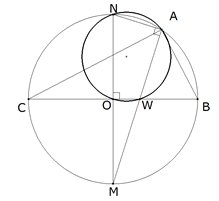
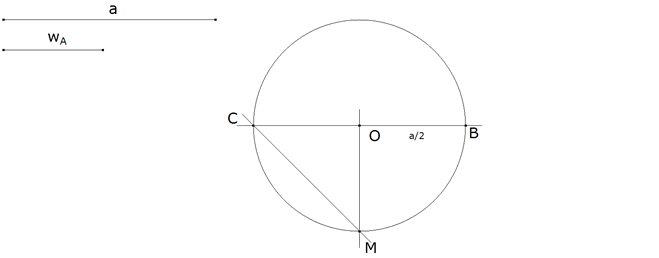
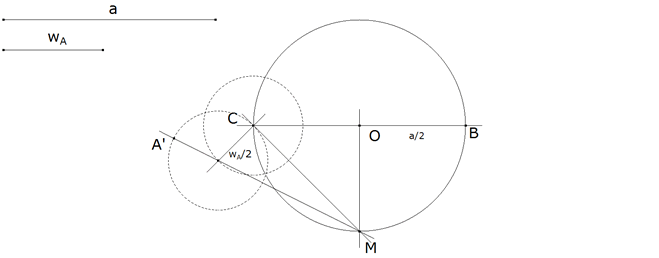
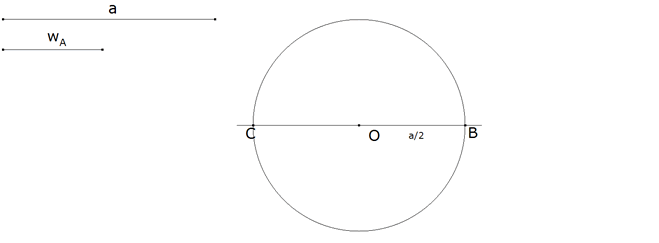Figura 8

Dado a, con centro en un punto O trazamos un círculo de radio OB=a/2 y diámetro BC=a.

Figura 9

La mediatriz de BC corta al círculo en M, entonces MC es la diagonal de un cuadrado de lado a/2.

Figura 10

Con centro  sobre la perpendicular a MC por C y radio W_A/2 trazamos el círculo que pasa por C. La recta por M y el centro de este círculo corta a este último en A'. MA' Es la magnitud buscada.

Figura 10

Con centro en M, circunferencia de radio MA’ que corta al círculo inicial en A.

ABC es el triángulo buscado.

La segunda intersección nos daría la segunda solución simétrica a la primera respecto a la mediatriz de BC.