Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 227

416 Construïu un triangle rectangle conegudes la hipotenusa i la bisectriu de l’angle recte.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solució deRicard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Siga el triangle rectangle , .

Aplicant el teorema de Pitàgores al triangle rectangle :

DeternineM el valor de la bisectriu en funció dels costats.

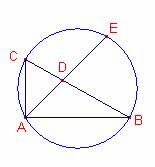
Considerem la circumferència circumscrita al triangle .

La recta que passa pels punts A, D talla la circumferència en el punt E.

Els triangles i són semblants (tenen els mateixos angles). Aplicant el teorema de Tales:

.

(1)

Aplicant la potència del punt D respecte de la circumferència circumscrita al triangle :

(2)

Substituint l’expressió (2) en l’expressió (1):

(3)

Calculem el valor de la bisectriu en funció dels costats.

Per la propietat de la bisectriu:

.

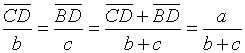Aleshores:

, (4)

Substituint les expressions (4) en l’expressió (3):

Aplicant el teorema de Pitàgores al triangle rectangle

.

Simplificant:

.

Resolent l’equació en la incògnita bc:

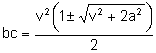
Considerem els sistemes:

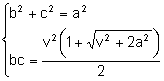
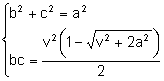
Per resoldre’l considerem el sistema:

Les solucions (reals positives) del qual són:

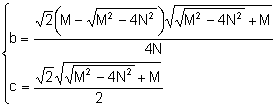
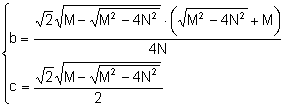
Notem que els la intersecció d’una circumferència i una hipèrbola.