Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 227

416 Construir un triángulo rectángulo conociendo la hipotenusa y la bisectriz del ángulo recto.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución deRicard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València) :

Siga el triángulo rectángulo , .

Aplicando el teorema de Pitágoras al triángulo rectángulo :

Determinemos el valor de la bisectriz en función de los lados.

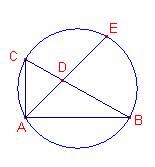
Consideremos la circunferencia circunscrita al triángulo .

La recta que pasa por los puntos A, D corta la circunferencia en el punto E.

Los triángulos y son semejantes (tienen los mismos ángulos). Aplicando el teorema de Tales:

.

(1)

Aplicando la potencia del punto D respecto de la circunferencia circunscrita al triángulo :

(2)

Substituyendo la expresión (2) en la expresión (1):

(3)

Calculemos el valor de la bisectriz en función de los lados.

Por la propiedad de la bisectriz:

.

Entonces:

, (4)

Substituyendo las expresiones (4) en la expresión (3):

Aplicando el teorema de Pitágoras al triángulo rectángulo

.

Simplificando:

.

Resolviendo la ecuación en la incógnita bc:

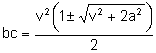
Consideremos los sistemas:

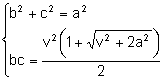
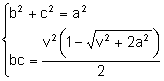
Para resolverlos consideremos el sistema:

Las soluciones (reales positivas) del cual son:

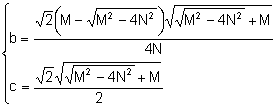
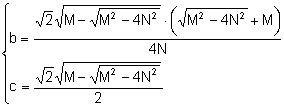
Notemos que las soluciones son la intersección de una circunferencia y una hipérbola.