Propuesto
por José María Pedret, ingeniero naval (Esplugues de Llobregat,
Barcelona)
Problema 227.- 416 Construir un
triángulo rectángulo conociendo la hipotenusa y la bisectriz del ángulo recto. Sapiña,
J. (1955): Problemas Gráficos de Geometría,Litograf.
Madrid.(Juan Sapiña Borja,
Aparejador, Perito Industrial, Profesor )
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca (20 de febrero de 2005).
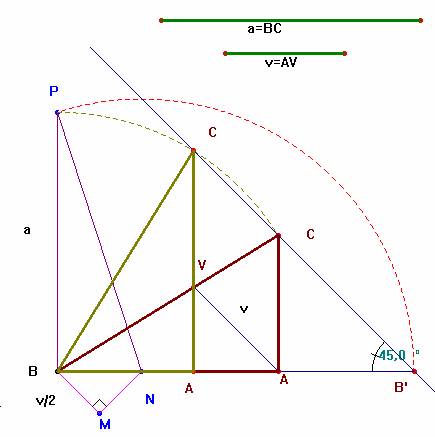
El
teorema de los senos aplicado al triángulo AVB nos da, de inmediato, v=AV
=
(1) (triángulo marrón). Por el teorema de Pitágoras en ABC
se obtiene 2bc= (b+c)2-a2
y por tanto la bisectriz puede ponerse como
(2).
En
(2) la única cantidad desconocida es x = b+c. Operando resulta:
x2 ─ 
vx ─ a2
= 0 (3)
ecuación cuya solución positiva es
x=b+c=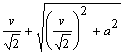
que puede construirse como se
indica a continuación:
El
primer sumando es la hipotenusa BN de un triángulo rectángulo cuyos
catetos BM, MN son iguales a v/2.
El
segundo es la hipotenusa NP de un triángulo rectángulo de catetos BN ─el anterior─ y BP =a.
Conocido
b+c =BB’ se puede construir el triángulo BCB’ del que se conocen
los lados BB’ = b+c, BC = a y el ángulo BB’C
= 45º.
Hay
dos triángulos BCB’ como puede observarse en el dibujo. El pie de la
altura desde C es el vértice A del triángulo solución.
Las dos soluciones se obtienen permutando B y
C.