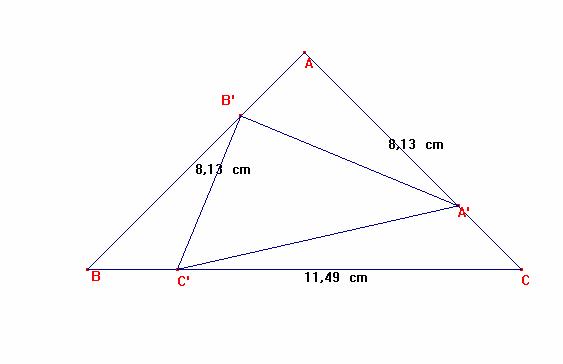
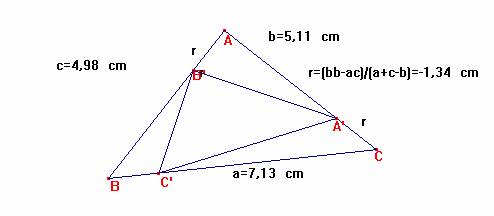
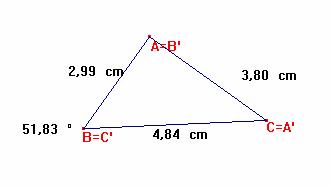
Problema 228

Sea ABC un triángulo rectángulo en A. Sea a>b>=c.

Hallar x real tal que si tomamos a+x, b+x, c+x,

prolongando una longitud x a a desde B, y obteniendo C' ,

prolongando una longitud x a b desde C y obteniendo A',

y prolongando una longitud x a c desde A y obteniendo B',

el triánguloA'B'C' es rectángulo en B'.

Romero, J.B. (2005): Comunicación personal.

Solución de Juan Bosco Romero Marquéz, profesor colaborador de la Universidad de Valladolid

Sea a=BC, b=AC, c=AB. Con <A=90º.

Sea r=C’A’, q=B’A’, y p= C’B’.

Deseamos que A’B’C’ sea rectángulo en B’; r² =p² + q² [1]

Cos C= b/a, cos B= c/a.

En el triángulo C’B’B aplicamos el teorema del coseno:

p ²= (x+c) ² + x² – 2 (x(c+x)) cos B= c² +2cx + 2x² + 2 x(x+c)c/a =

(ac²+2acx+2x² a+ 2 x c² + 2 x ² c)/a

El triángulo B’AA’ es rectángulo en A:

q² = x ² + (b+x) ² = 2 x ² + 2bx + b²

En el triángulo C’A’C aplicamos el teorema del coseno:

r ²= (x+a) ² + x² – 2 (x(a+x)) cos C= a² +2ax + 2x² + 2 x(x+a)b/a =

(a³+2a²x+2x² a+ 2 abx + 2 x ² b)/a

Dado que tenemos [1], es:

r² = p² + q²

a³+2a²x+2x² a+ 2 abx + 2 x ² b = = 2 ax ² + 2abx + b² a + ac²+2acx+2x² a+ 2 x c² + 2 x ²c

Simplificando:

a³+2a²x + 2 x ² b = = 2 ax ² + b² a + ac² + 2acx + 2 x c² + 2 x ²c

a³+2a²x + 2 x ² b = 2 ax ² + a³ + 2acx + 2 x c² + 2 x ²c

Simplificando de nuevo, y tomando x y x² factores comunes:

x ² ( 2 b – 2 a – 2c) + x( 2 a² – 2 a c – 2 c ²) = 0.

x=0 es una solución, y queda:

x ( b – a – c) + ( a² – a c – c ²) = 0.

x = ( b² – a c) / ( a + c – b)

Puede ser:

x > 0 si b² -ac>0, caso que significa que :

B’ es exterior a BA,

C’ exterior a CB

y A’ exterior a AC, como en la primera figura.

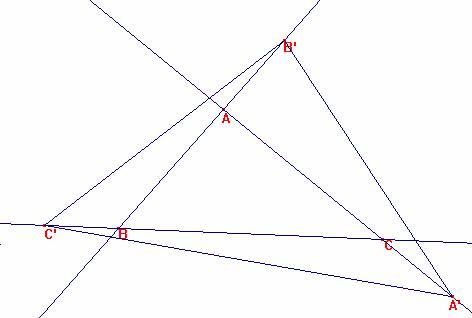
x<0, si b²-ac<0, caso que significa que el

triángulo A’B’C’ rectángulo es interior e inscrito

al ABC, como se muestra en la figura:

x=0 si b² – ac =0; es decir, si los lados c, b y a están en progresión geométrica:

b² – ac =0 implica : a² – ac - c² =0; es decir, (a/c) ² – (a/c) -1=0

Luego es .

cos B=1,247/2; B=51,83º

Si el triángulo es rectángulo e isósceles,