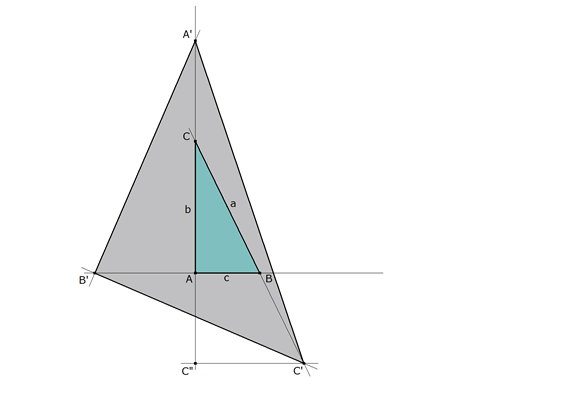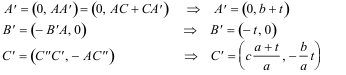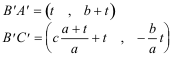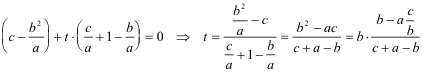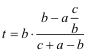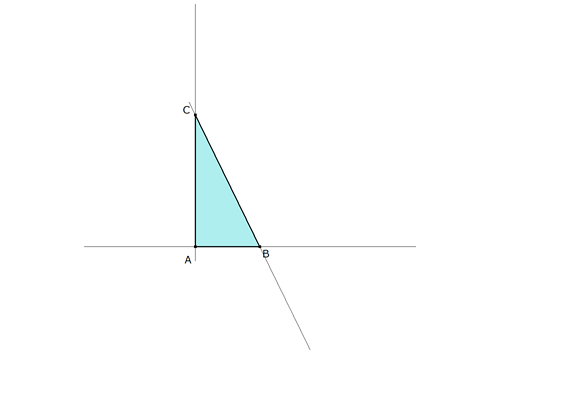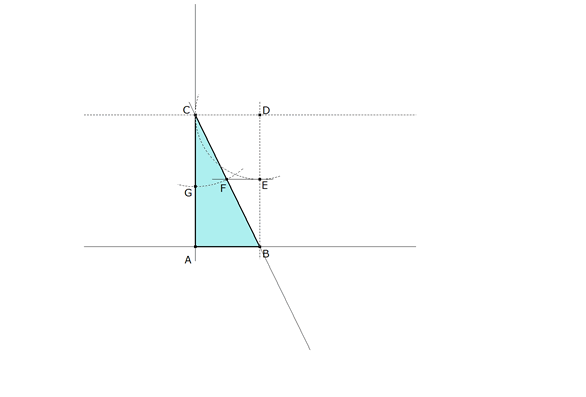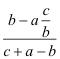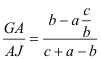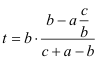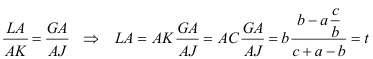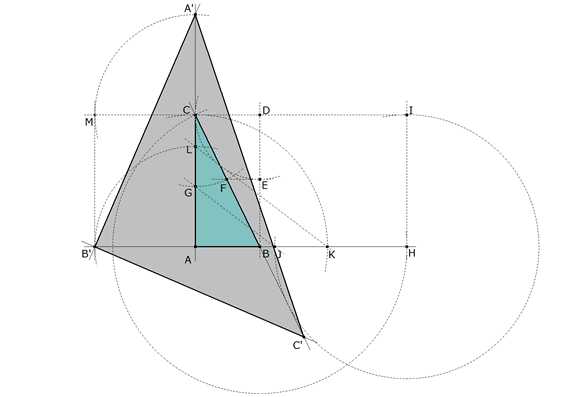Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid Problema 228 Sea ABC un triángulo rectángulo en A. Sea a > b >= c. Hallar t real tal que si tomamos a+t, b+t, c+t, prolongando una longitud t a a desde B, y obteniendo C', prolongando una longitud t a b desde C y obteniendo A', y prolongando una longitud t a c desde A y obteniendo B', el triángulo A'B'C' es rectángulo en B'.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2005) |
|
INTRODUCCION |
|
Frente al avance, en su tiempo, de la Geometría Analítica; decía Poncelet que una de las principales herramientas para la resolución de problemas en geometría son las proporciones; pero que incluso las proporciones era un álgebra de segmentos disfrazada. Ya me perdonará Poncelet porque voy a hacer exactamente al revés: empezaré con un poco de álgebra, obtendré una serie de proporciones y las construiré con regla y compás (exactamente CABRI II Plus). Francisco Javier García Capitán usa regularmente y con mucha ventaja este tipo de método. A él dedico pues esta solución si es que tiene el suficiente valor para ser dedicada. Las líneas básicas se dibujarán en trazo continuo y las líneas auxiliares en discontinuo. No se dibujarán los círculos completos y en su lugar se trazarán arcos de círculo. Espero que así no se “amontonen” una multitud de trazos que hacen ininteligible el dibujo final. Las construcciones se efectuarán directamente sobre el triángulo original. Con ello obtendremos el triángulo solución sobre la propia figura. El orden de aparición de los puntos auxiliares en la construcción será el orden alfabético. |
|
DISCUSION |
|
Dibujamos un triángulo rectángulo y lo “deformamos” como dice el enunciado. Pensando en un sistema de referencia apropiado adoptaremos a A como origen, AB como eje de abscisas y AC como eje de ordenadas. Como es habitual
figura 1 Suponemos el problema resuelto. Entonces, de acuerdo con el enunciado.
Las coordenadas de A’, B’ C’ son
Hemos determinado C”C’ observando la figura
Y también AC”
Determinaremos ahora el valor de t que hace que A’,B’,C’ sea rectángulo en B’.
Determinamos B’A’ y B’C’
Expresaremos la perpendicularidad de B’A’ y B’C’ haciendo que su producto escalar se anule
La primera raíz es t=0, que no es más que el triángulo original. La segunda raíz nos da la solución
|
|
SOLUCION |
|
Si sabemos construir t con regla y compás obtendremos el triángulo solución
Dibujamos el enunciado A,B,C |
|
|
|
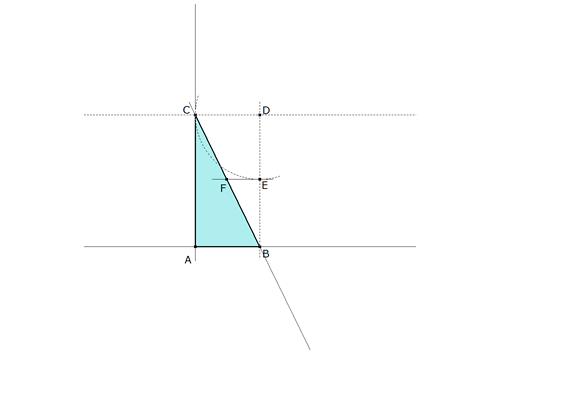
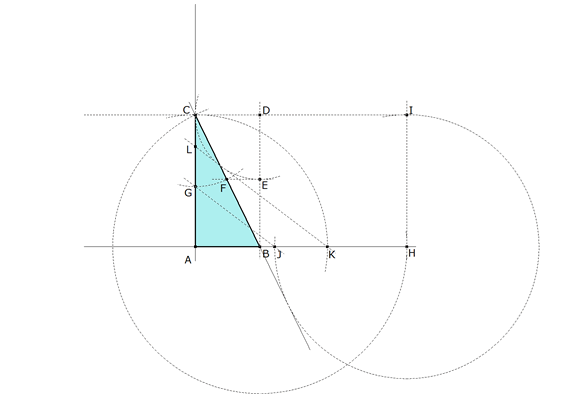
figura 3 Completamos el paralelogramo y obtenemos el punto D. Círculo de centro en D y radio DC corta a DB en E. Paralela por E a AB que corta a CB en F. CF es el valor buscado
|
|
|
|
figura 4 Con centro en C, círculo de radio CF que corta a CA en G, GA es el valor buscado
|
|
|
|
figura 5 Con centro en B, círculo de radio BC que corta a AB en H; por H paralela a CA que corta a CD en I y ahora con centro en H círculo de radio HI que corta a AB en J. AJ es el valor buscado
|
|
|
|
figura 6 La relación pedida según hemos visto en los dos apartados anteriores es
La recta JG define la dirección que proporciona esa razón. |
|
|
|
figura 7 Con centro en A, círculo de radio AC que corta a AB en K. Paralela por K a JG. que corta a CA en L. AL es el parámetro t buscado.
Obtenido el parámetro t, es sencillo dibujar el triángulo pedido. |
|
DIBUJO DEL TRIANGULO A PARTIR DE t |
|
figura 8 B’ Con centro en A, círculo de radio AL=t que corta a AB en B’. A’ Por B’ paralela a CA que corta a CD en M; con centro en C, círculo de radio CM que corta a CA en A’. C’ Como B’A’C’ debe ser rectángulo, por B’ perpendicular a A’C’ que corta a BC en C’ UNIENDO A’B’C’ OBTENEMOS EL TRIANGULO BUSCADO |