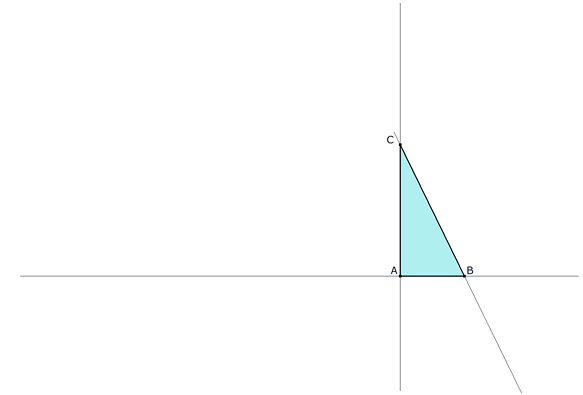Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 228

Sea ABC un triángulo rectángulo en A. Sea a > b >= c.

Hallar t real tal que si tomamos a+t, b+t, c+t, prolongando una longitud t a a desde B, y obteniendo C', prolongando una longitud t a b desde C y obteniendo A', y prolongando una longitud t a c desde A y obteniendo B', el triángulo A'B'C' es rectángulo en B'.

Romero, J.B. (2005): Comunicación personal.

Segunda solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de marzo de 2005)

INTRODUCCION - DISCUSION

Ya que el nombre de esta página de problemas auspiciada por RICARDO BARROSO CAMPOS es

figura 1

Vamos pues a realizar una solución, no posible con regla y compás; pero si con CABRI II Plus.

Para ello y siguiendo el enunciado, utilizaremos un parámetro t cualquiera y obtendremos nuestros puntos en función de t:

Determinaremos ahora un punto B”(t) que con los dos anteriores cumpla con el enunciado; pero relajando una de las condiciones. Nosotros relajamos la condición de que B”(T) esté sobre AB

Imponemos ahora la primera condición relacionada con la formación del triángulo rectángulo que exige que B”(t) esté sobre el círculo de diámetro A”(t)C”(t)

Imponemos también la segunda condición que nos dice que B”(t) está a distancia t de A

Por lo tanto el lugar geométrico de las posiciones de B”(t) es la siguiente intersección

Reintroduciendo ahora la condición relajada más arriba tenemos la solución B’ para el valor del parámetro t_s

El triángulo A’B’C’ es la solución buscada.

Utilizaremos la herramienta lugar geométrico y la intersección de lugares geométricos con otros objetos, ambas disponibles en CABRI II Plus.

SOLUCION

figura 2

Dibujamos el enunciado A,B,C.

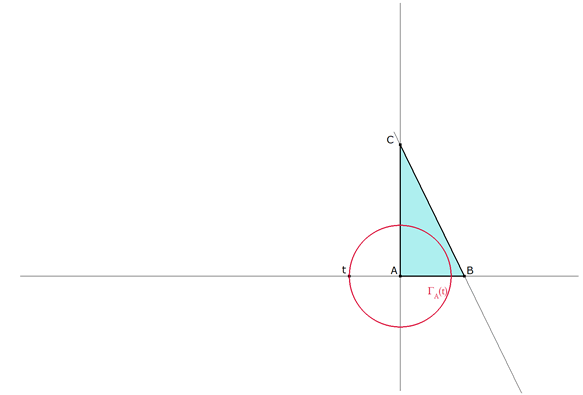
DEFINICION DEL PARAMETRO t - DIBUJO DE Γ_A(t)

figura 3

Sobre AB y tal como se aprecia en la figura, definimos un parámetro t de acuerdo al enunciado. (Punto sobre un objeto)

Al mismo tiempo trazamos Γ_A(t), el círculo de centro en A y radio t. (Círculo)

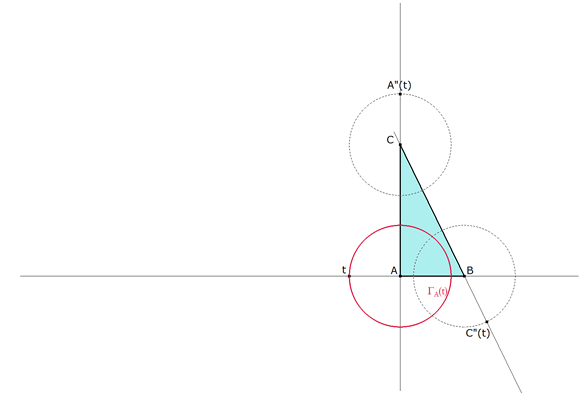
DETERMINACION DE A”(t) y C”(t)

figura 4

Con centro en C, círculo de radio t que corta a CA en A”(t). (Compás + Punto(s) de intersección)

Con centro en B, círculo de radio t que corta a BC en C”(t). (Compás + Punto(s) de intersección)

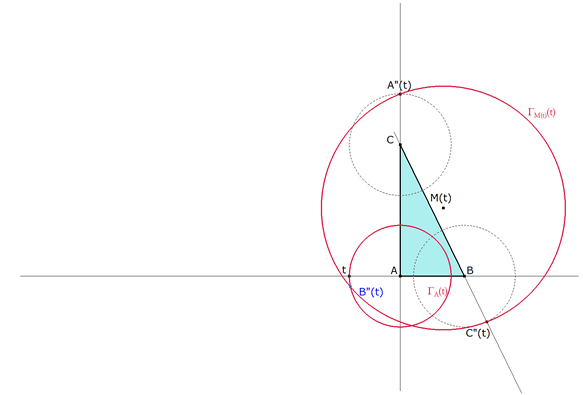
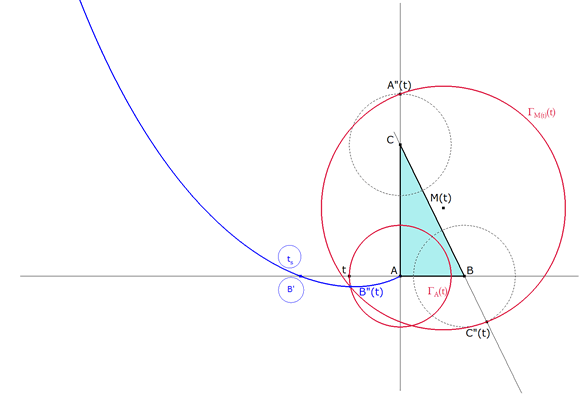
TRAZADO DE Γ_M(T)(t) - DETERMINACION DE B”(t)

figura 5

Con centro en M(t), punto medio de A”(t) y C”(t), se traza Γ_M(T)(t) el círculo de diámetro A”(t)C”(t). (Punto medio +Círculo)

(Punto(s) de intersección)

TRAZADO DEL LUGAR GEOMETRICO DE B”(t)

figura 6

Trazado en azul, tenemos el lugar geométrico del punto B”(t) al desplazar t sobre AB. (Lugar)

Lugar que corta a AB en el punto B’ de parámetro t_s. (Punto(s) de intersección)

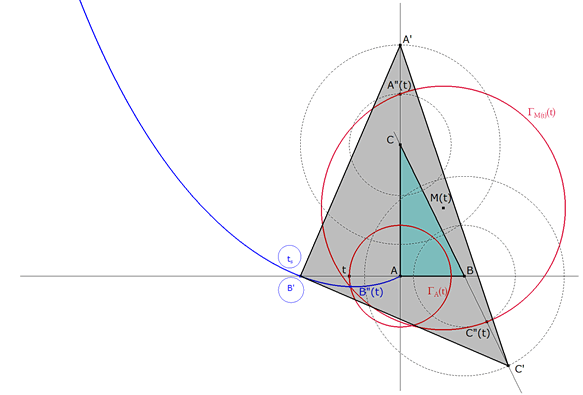
DIBUJO DEL TRIANGULO A PARTIR DE t_s

figura 7

B’

Con centro en A, círculo de radio t_s que corta a CA en A’. (Compás + Punto(s) de intersección)

C’

Con centro en B, círculo de radio t_s que corta a BC en C’. (Compás + Punto(s) de intersección)

UNIENDO A’B’C’ OBTENEMOS EL TRIANGULO BUSCADO