Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 228.- Sea ABC un triángulo rectángulo en A. Sea a>b>=c. Hallar x real tal que si tomamos a+ x, b+ x, c+ x, prolongando una longitud x a a desde B, y obteniendo C' , prolongando una longitud x a b desde C y obteniendo A', y prolongando una longitud x a c desde A y obteniendo B', el triángulo A'B'C' es rectángulo en B'.   Romero, J.B. (2005): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

 

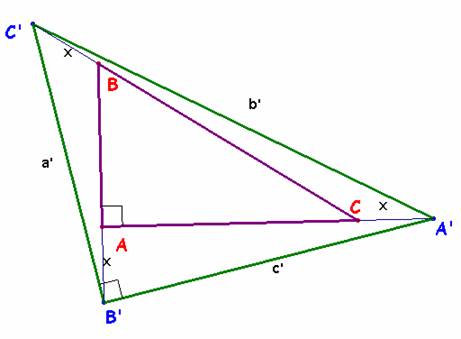
                Llamando a cada lado con la letra del vértice opuesto, la aplicación del teorema del coseno a los tres triángulos externos formados en torno al inicial, más el triángulo final, A’B’C’  nos proporcionan cuatro ecuaciones con cuatro incógnitas: los tres lados del triángulo A’B’C’ y el valor del segmento x buscado.  Ese sistema de ecuaciones de segundo grado, tiene siempre una solución que es x=0, con lo que nos quedamos con el triángulo rectángulo del enunciado. Eliminada esta solución habremos de obtener otra solución para x que es la que debemos construir.

 Estas relaciones son las siguientes:

c’ 2 = x2 + (b+x)2                              (1)

a’ 2 = x2 +(c+x)2 + 2x(c+x)cos B     (2)

b’ 2 = x2 +(a+x)2 + 2x(a+x)cos C    (3)

a’ 2 = b’ 2 ─ c’ 2                                 (4)

 

                De (2) y (3) se obtiene:       b’ 2 ─ a’ 2 = (a+x)2 ─ (c+x)2 +2x· [(a+x)·b/a ─(c+x)·c/a] .

Después de varios cálculos con un poco de paciencia llegamos a

b’ 2 ─ a’ 2 = 2·x2  + 2(a ─c + b ─c2/a) x + b2         (5)

                Por otra parte  c’ 2 = x2 + (b+x)2 = 2x2 + 2bx + b2.                                  (6)

Igualando (5) y (6) y simplificando lo que se pueda sale:

2(a─b+c)x2 + 2(─a2+ac+c2)x=0 

Dividiendo por 2x (eliminando la solución x=0) y utilizando b2 =a2 ─ c2, obtenemos finalmente una ecuación de primer grado de donde se despeja el siguiente valor para el segmento x:

.

Para construir este segmento lo ponemos como diferencia de dos segmentos,  x’= y x”= cuya construcción gracias al teorema de Thales, es muy sencilla como se muestra en la figura final.

 Se toma un segmento l cuya longitud es a─b+c. En sendas semirrectas de origen  O se llevan segmentos OB, OC yOL de longitudes respectivas b, c y l. El teorema de Thales completa la construcción de dos puntos X’, X”  tales que el segmento X’X” es igual a x.