 1.
Llamemos x al ángulo buscado. Experimentando con Cabri
podemos encontrar que x=20º es la solución del problema.
Tratemos de llegar a este resultado mediante trigonometría:
1.
Llamemos x al ángulo buscado. Experimentando con Cabri
podemos encontrar que x=20º es la solución del problema.
Tratemos de llegar a este resultado mediante trigonometría:
Problema 229 de triánguloscabri |
|
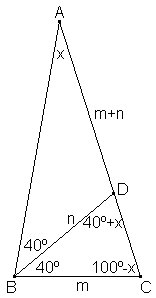
Se tiene un triángulo ABC y se sabe que BC = m, la bisectriz BD = n, DA= m + n, ÐABD = ÐDBC = 40º. Calcular ÐBAC. |
Solución de Francisco Javier García Capitán
 1.
Llamemos x al ángulo buscado. Experimentando con Cabri
podemos encontrar que x=20º es la solución del problema.
Tratemos de llegar a este resultado mediante trigonometría:
1.
Llamemos x al ángulo buscado. Experimentando con Cabri
podemos encontrar que x=20º es la solución del problema.
Tratemos de llegar a este resultado mediante trigonometría:
Usando el teorema de los senos con los triángulos BCD obtenemos:
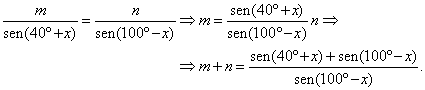
Usando también el teorema de los senos, pero con el triángulo BDA,
![]()
Por tanto, x es solución de la ecuación
![]()
Para x=20º resulta la igualdad
![]()
que podemos razonar usando la identidad ![]() ,
ya que entonces la igualdad anterior se convierte en esta otra
,
ya que entonces la igualdad anterior se convierte en esta otra
![]()
que a su vez es cierta por ser ![]() y
y
![]()
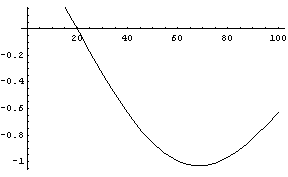
2. ¿Habrá alguna solución distinta de 20º? No he encontrado una forma más satisfactoria de responder a esta pregunta que usar Mathematica para representar gráficamente la ecuación y "ver" que sólo hay una solución.
![]()
![]()
![]()