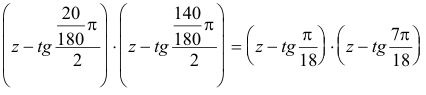Problema 229 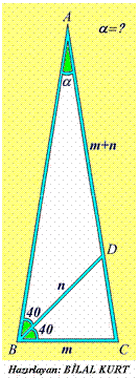
Se tiene un triángulo ABC y se sabe que BC =m, la bisectriz BD=n, DA= m+n, <ABD=<DBC=40º. Calcular <BAC. Del "sitio" turco:KULUBU (2005): http://www.matematik.kulubu.com/ Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de abril de 2005) |
|
Antes de empezar debo decir que mi resolución original de este problema no tenía la calidad de la que aquí presento. |
|
INTRODUCCION - DISCUSION - SOLUCION |
|
Descomponemos el triángulo dado en dos triángulos:
Aplicamos el teorema de los senos en dos de los triángulos; el tercero proporcionaría ecuaciones redundantes. En ABD se cumple
En DBC se cumple
Restando numeradores y denominadores en (2)
Y dividiendo m.a.m. en (3)
Igualando (4) y (5)
|
|
NUMERO DE SOLUCIONES DE LA ECUACION (6) |
|
Para estudiar la ecuación (6) la desarrollaríamos en función del seno y el coseno de α. Racionalizaríamos luego la expresión mediante el cambio
y el seno queda como
mientras que el coseno queda como
y sustituyendo en (6)
Por lo que nos queda un polinomio de cuarto grado en z. LA ECUACION TIENE COMO MAXIMO CUATRO SOLUCIONES Ahora podemos resolver la ecuación (“muy pesado”) y habríamos acabado. Determinaremos un método fácil de buscar dos raíces y una vez obtenidas podríamos eliminar estas raíces y resolver cómodamente un problema de segundo grado. |
|
BUSQUEDA DE LAS RAICES |
|
Recordando que
y sustituyendo en (6)
Agrupando adecuadamente los miembros de (12), obtenemos tres ecuaciones auxiliares
Teniendo ahora presente que
de la primera ecuación auxiliar
de la segunda ecuación auxiliar
y de la tercera ecuación auxiliar
LA PRIMERA SOLUCION ES
Pues satisface las tres ecuaciones auxiliares
Agrupando nuevamente los miembros de (12), obtenemos tres ecuaciones más
de la primera y aumentando el primer ángulo en 360
de la segunda, aumentando en 360 y tomando el primer ángulo negativo
de la tercera tomando el primer ángulo negativo
LA SEGUNDA SOLUCION NO ES VALIDA EN ESTE TRIANGULO
Obtenidas estas soluciones podríamos reducir la transformada en z de la ecuación (6) dividiéndola por
Y obtendríamos un polinomio de segundo grado del que obtendríamos el resto de soluciones ¡exactas! De estas dos soluciones sólo hay una más válida LA TERCERA SOLUCION NO ES VALIDA YA QUE ESTA EN EL INTERVALO
LA CUARTA SOLUCION NO ES VALIDA ; PUES
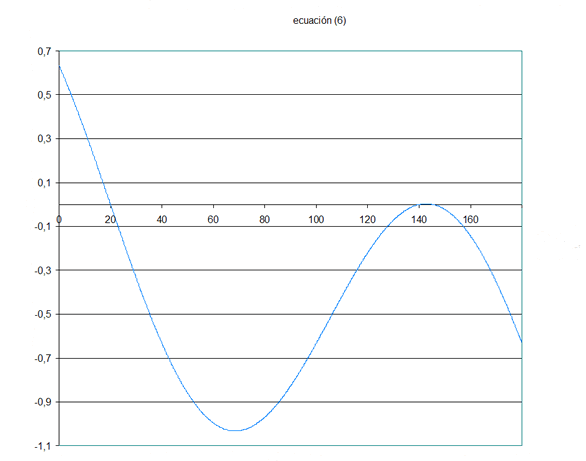
Una comprobación adicional nos la da la representación gráfica de la ecuación (6) que sólo se anula TRES veces entre 0 y 180 grados
|
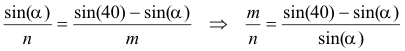 (4)
(4)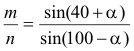 (5)
(5)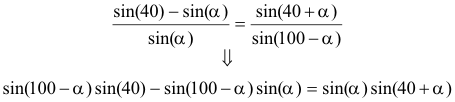 (6)
(6)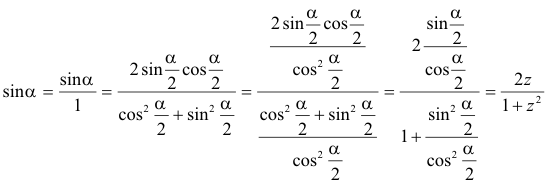
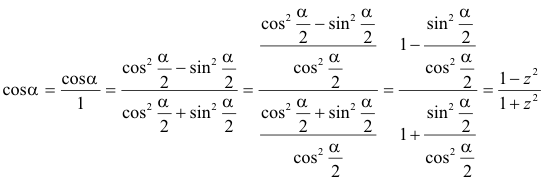
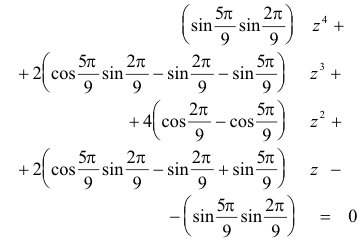
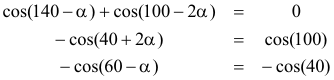 (13)
(13)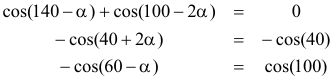 (19)
(19)