Problema 229
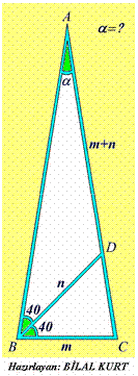
Se tiene un triángulo ABC y se sabe que BC =m, la bisectriz BD=n, DA= m+n, <ABD=<DBC=40º. Calcular <BAC. Del "sitio" turco:KULUBU (2005): http://www.matematik.kulubu.com/ Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de abril de 2005) |
|
INTRODUCCION |
|
Como no he sido capaz de encontrar una solución con regla y compás, me he dedicado a establecer una solución 100% CABRI II.
|
|
SOLUCION |
|
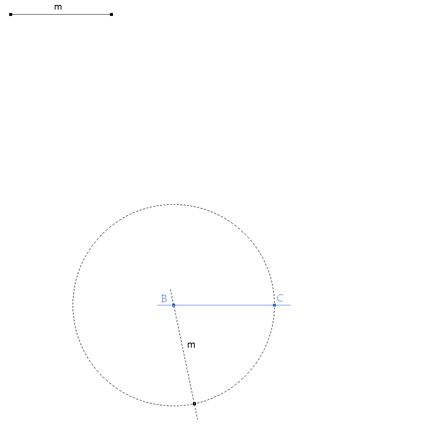
figura 2 Tomaremos m como parámetro básico. (Segmento) Por un punto B trazamos una recta. (Recta)
|
|
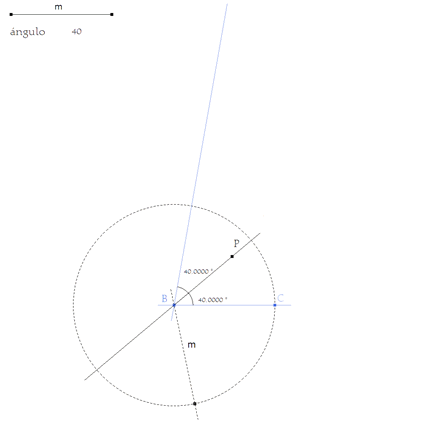
figura 3 Representando el ángulo de 40 grados. (Texto+Número) Giramos la recta BC en torno a B 40 grados. (Rotación) Seguimos girándola 40 grados más entorno a B. (Rotación)
Hemos formado un ángulo de 80 grados con su bisectriz.
|
|
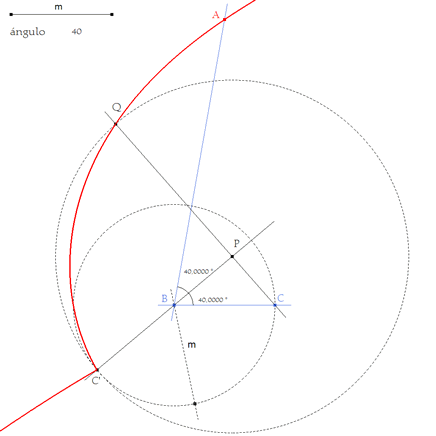
figura 4 El círculo de centro B y radio m corta a la bisectriz en C’. (Punto(s) de intersección)
|
|
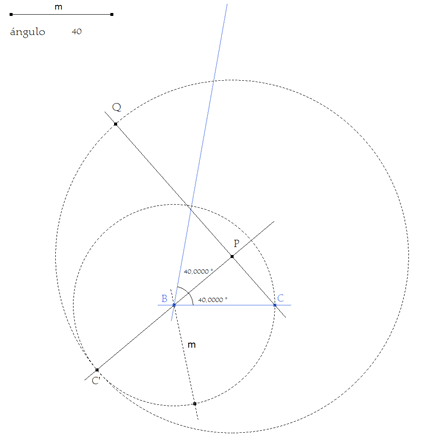
figura 5 Si fuera solución Q estaría sobre el lado del ángulo que forma 80 grados con BC. Por tanto, hallamos el lugar geométrico del punto Q cuando P se desplaza sobre la bisectriz. (Lugar) Este lugar corta en A al lado que forma 80 grados con BC. (Punto(s) de intersección)
|
|
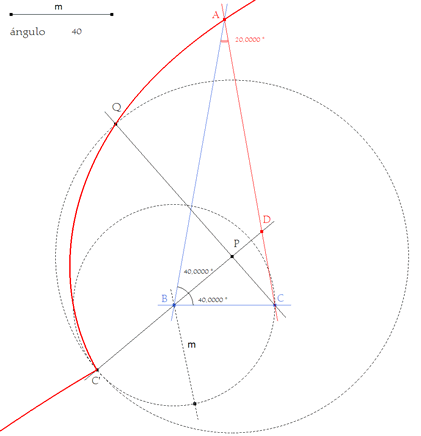
figura 6 Obtenido A Trazamos el lado CA que corta a la bisectriz en D. (Rectas+Punto(s) de intersección)
|