Problema 230
Calcular la hipotenusa y cateto de un triángulo rectángulo de perímetro 60 cms y tal que la altura del ángulo recto mide 12 cms.

MATEMATICA ELEMENTAL (1947). EJERCICIOS ELEMENTALES RESUELTOS.

Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid). Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española.
Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

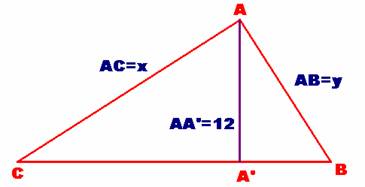
Primera Solución:

Como quiera que los triángulos AA’B y AA’C tienen un lado entero AA’ =12 y son semejantes al inicial ABC, con perímetro también un valor entero, no hay más remedio que el triángulo inicial ABC sea pitagórico, relacionado con el número 12 = 3∙4 y por tanto del tipo 3k, 4k; 5k.

Por tanto, como su perímetro es 60, tenemos que 3k+ 4k+ 5k = 60; k= 5 y así el triángulo ABC es el de longitudes iguales a 15, 20 ; 25.

Segunda Solución:

Con los datos del problema, obtenemos las siguientes relaciones de interés en el triángulo rectángulo ABC, recto en A:

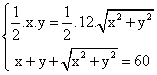, que representan, respectivamente las expresiones del área y el perímetro de dicho triángulo. De dichas relaciones, deducimos que:

; ;

Despejando y² en la primera ecuación del sistema, obtenemos:

Igualamos estas dos últimas expresiones de y²,

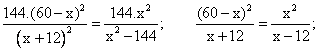
Simplificando los cálculos pertinentes, obtenemos la ecuación de segundo grado siguiente:

x² −35x +300 = 0, cuyas soluciones son 20 y 15.

Para x= 20, tenemos y= 15.

Para x= 15, tenemos y= 20.

En definitiva, los lados del triángulo rectángulo son 15, 20 y 25.