La altura
relativa a la hipotenusa puede calcularse usando triángulos semejantes
y resulta como indica la figura de la derecha. Entonces, el problema se reduce
a resolver el sistema:
Problema 230 de triánguloscabri |
|
189. Calcular la hipotenusa y cateto de un triángulo rectángulo de perímetro 60 cms y tal que la altura del ángulo recto mide 12 cms. |
|
Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española. Propuesto por Maite Peña Alcaraz. |
Solución de Francisco Javier García Capitán
Solución numérica:
La altura
relativa a la hipotenusa puede calcularse usando triángulos semejantes
y resulta como indica la figura de la derecha. Entonces, el problema se reduce
a resolver el sistema:
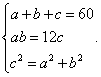
Para ello, hacemos:
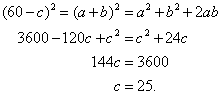
Ahora, por ser 
y 
,
tendremos que a y b son las soluciones de la ecuación
, es
decir, los catetos son a=15 y b=20 o viceversa.
Solución gráfica:
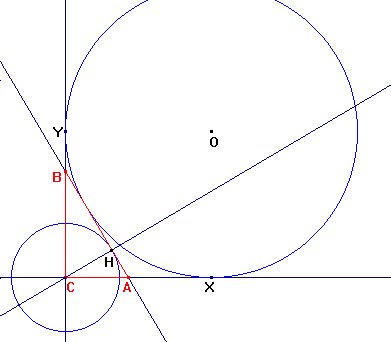Usamos que
el semiperímetro s es la distancia del vértice C a los puntos
de contacto X e Y de la circunferencia exinscrita correspondiente
al vértice C con los lados CA y CB.
Entonces, en la figura será CX=CY=s. La distancia CH es dada, por lo que H estará en una circunferencia de centro C y radio CH.
Por tanto, lo único que tenemos que hacer dados s y CH es dibujar el cuadrado CXOY de lado s, la circunferencia con centro O y radio s, la circunferencia con centro C y radio CH, y la tangente común a ambas circunferencias, que determinará con los lados CX y CY los vértices del triángulo buscado.
Applet de CabriJava: Puedes modificar el perímetro y la altura sobre la hipotenusa: