Problema 231
Construir un triángulo conociendo los pies de las tres alturas.

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)
Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Solución:

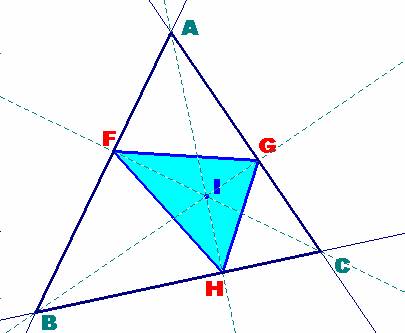
Los pies de las alturas, F, G y H de un triángulo dado ABC son los vértices del triángulo órtico.

Sabemos que las bisectrices del triángulo órtico se corresponden con las alturas del triángulo inicial. De este modo la construcción del triángulo ABC no presenta dificultad alguna.

Veamos esta propiedad con mayor detalle:

Circunferencia circunscrita a un triángulo dado. Relaciones entre las alturas.

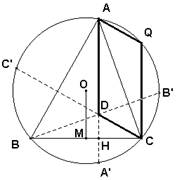Sea el triángulo ABC y D su ortocentro. Consideremos la circunferencia circunscrita a dicho triángulo, de centro O.

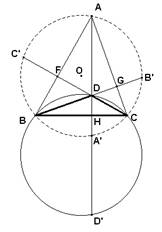
1) Si AD corta al lado BC en H, y a la circunferencia en A', entonces DH = HA'.
2) Si M es el punto medio de BC, entonces AD = 2×OM

Dem.-

1º) Si AD corta al lado BC en H, y a la circunferencia en A', entonces DH = HA'.
Esto es debido a la congruencia de los triángulos rectángulos en H, HDC y HA'C. Tienen el lado común HC, y además son iguales los ángulos HCD y HCA', por ser ambos iguales al ángulo HAB.

2º) Si M es el punto medio de BC, AD = 2×OM.
Si la perpendicular por C a BC corta a la circunferencia en Q, entonces QB es un diámetro de la misma, y por tanto, QB pasa por O. Al considerar el triángulo BCQ, se tendrá consecuentemente que OM es la paralela media del lado QC; QC = 2×OM. Por otra parte, si trazamos el cuadrilátero QADC resulta ser un paralelogramo, pues QC y AD son ambos perpendiculares al lado BC, y lo mismo sucede con AQ y DC al ser también perpendiculares al lado AB. Luego entonces se tendrá que AD =QC =2×OM

3) Los seis arcos de circunferencias determinados por los puntos A, B, C y por los extremos de las prolongaciones de sus respectivas alturas A', B', C' son iguales dos a dos.
Basta observar la igualdad de los siguientes ángulos <BAC=<A'CB=<BCC'.

4) Considerando tres puntos cualesquiera de A, B, C, D el cuarto punto será el ortocentro del triángulo determinado por los primeros puntos elegidos.

5) La altura AHD' es dividida por la base AB en dos partes iguales.
Teniendo en cuenta los resultados anteriores, si consideramos la circunferencia circunscrita al triángulo DBC entonces AH = HD'.

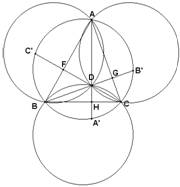
6) Una misma circunferencia circunscribe a los triángulos ABC, ABD, BCD y ACD.

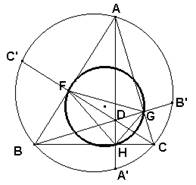
7) Las alturas son bisectrices de los ángulos del triángulo FGH formado por los pies de las alturas. Este triángulo se llama triángulo órtico. Sea el triángulo A'C'B'. Entonces CC' es bisectriz del ángulo A'C'B' pues CA' = CB'. CF es bisectriz del ángulo F formado por las paralelas medias a dos de los lados del primer triángulo. Así se tendrá para los demás ángulos y alturas correspondientes.