Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 231

437 Construir un triángulo conociendo los pies de las tres alturas.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat.
(1 de abril de 2005)

TEOREMAS

Teorema I. ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 51)
En una misma circunferencia o en circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales, y a arcos iguales corresponden ángulos centrales iguales.

Teorema II. ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 53)
El lugar geométrico de los vértices de todos los ángulos directamente congruentes entre sí cuyos lados pasan por dos puntos fijos A y B, es un arco de circunferencia de extremos A y B, llamado arco capaz del ángulo sobre el segmento AB.

Teorema III. ( Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición Pág. 84)
Todo ángulo inscrito en una circunferencia es igual a la mitad del central que comprende el mismo arco.

DISCUSION

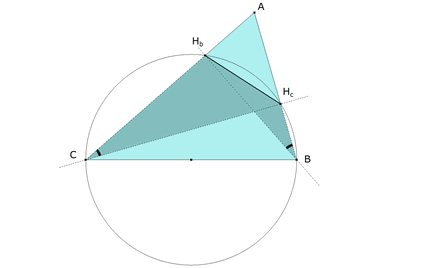
Supongamos el problema resuelto.

Figura 1

Si el arco es una semicircunferencia el ángulo central es π y por tanto si consideramos CH_bB inscrito en una circunferencia, el valor del ángulo es la mitad del central y ∠CH_bB=π/2.

Por lo tanto, podemos considerar al triángulo rectángulo como inscrito en un círculo cuyo diámetro es la hipotenusa y el vértice del ángulo recto sobre la circunferencia; y por lo tanto H_c como pie de altura es pie de la perpendicular desde C al lado AB y como tal es el vértice de un ángulo recto y de acuerdo con el párrafo anterior también está sobre la circunferencia de diámetro BC.

Figura 2

Existen por lo tanto tres círculos que pasan cada uno por dos pies de altura y por los vértices del lado del triángulo al que no pertenecen los pies de altura considerados.

Figura 3

Tomemos ahora, en el círculo H_bH_cBC, el segmento H_bH_c; los ángulos H_bCH_c y H_bBH_c son iguales y por lo tanto los ángulos ACH_c y H_bBA, son iguales.

Figura 4

En el círculo H_cH_aCA consideramos el segmento AH_c; los ángulos ACH_c y AH_aH_c son iguales.

Figura 5

Tomamos el segmento H_bA en el círculo H_aH_bAB; los ángulos H_bH_aA y H_bBA son iguales.

Figura 6

En la figura 5, los ángulos H_bH_aA y H_bBA son iguales

En la figura 3, los ángulos H_bBA y ACH_c, son iguales.
En la figura 4, los ángulos ACH_c y AH_aH_c son iguales.
Y así

∠H_bH_aA=∠H_bBA=∠ACH_c=∠H_bBA=∠ACH_c=∠AH_aH_c

por lo que deducimos que la altura AH_a es la bisectriz del ángulo H_bH_aH_c y a partir de aquí obtenemos BC como perpendicular a esa bisectriz. Y el mismo proceder nos conduciría a los otros dos lados.

SOLUCION

Figura 7

Dados H_a, H_b, y H_c trazamos la bisectriz de H_bH_aH_c. La perpendicular por H_a a esa bisectriz contiene a BC.

Figura 8

Podríamos proceder com en la figura anterior; pero la bisectriz de H_aH_cH_b es la altura por C y por lo tanto C será la intersección de esta última bisectriz y el lado BC.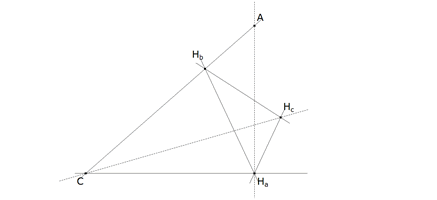

Figura 9

Aunque podemos repetir el proceso de la figura 7; el lado CA pasa por C y H_b. La recta CH_b corta a la altura AH_a en A.

Figura 10

Para concluir, obtenemos B como la intersección de la recta AH_c con BC

ABC es el triángulo buscado.