Problema 231

Proposat per José María Pedret, enginyer naval (Esplugues de Llobregat, Barcelona)

437 Construïu un triangle coneguent els peus de les tres altures.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

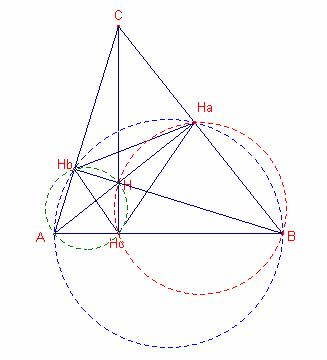
Triangle òrtic.

Donat el triangle  acutangle, siguen  els peus de les altures.

El triangle  s’anomena triangle òrtic del triangle .

Propietat:

Les bisectrius del triangle òrtic són les altures del triangle .

Demostració:

Provem que l’altura  és bisectriu de l’angle

,  aleshores el quadrilàter  és cíclic.

Aleshores,  (són angles interiors que abracen el mateix arc).

, , aleshores el quadrilàter  és cíclic.

Aleshores,         (1)

, , aleshores el quadrilàter  és cíclic.

Aleshores,       (2)

De (1) i (2)  , aleshores, l’altura  és bisectriu de l’angle

Per a les altres altures es provaria anàlogament.

Solució al problema:

Donats els tres peus de les altures , dibuixem les tres bisectrius interiors al triangle format pels 3 peus de les altures.

Dibuixem la recta perpendicular a la bisectriu del vèrtex  que passa per .

Dibuixem la recta perpendicular a la bisectriu del vèrtex  que passa per .

Dibuixem la recta perpendicular a la bisectriu del vèrtex  que passa per .

Les interseccions (dos a dos) d’aquestes perpendiculars ens dóna el triangle .

 

Figure barroso231.fig

Applet created on 2/04/05 by Ricard Peiró with CabriJava