Problema 231

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

437 Construir un triángulo conociendo los pies de las tres alturas.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

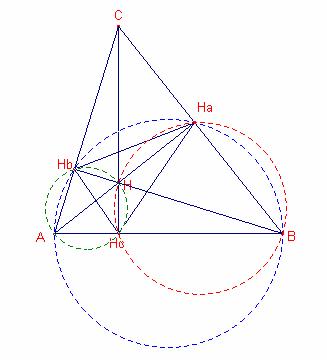
Triángulo órtico.

Dado el triángulo  acutángulo, sean  los pies de las alturas.

El triángulo  se llama triángulo órtico del triángulo .

Propietat:

Las bisectrices del triángulo órtico son las alturas del triángulo .

Demostración:

Probemos que l’altura  es bisectriz del ángulo

,  entonces el cuadrilátero  es cíclico.

Entonces,  (son ángulos interiores que abarcan el mismo arco).

, , entonces el cuadrilátero  es cíclico.

Entonces,         (1)

, , entonces el cuadrilátero  es cíclico.

Entonces,       (2)

De (1) i (2)  , entonces, la altura  es bisectriz del ángulo

Para las otras alturas se probaría análogamente.

Solución al problema:

Dados los tres pies de las alturas , dibujamos las tres bisectrices interiores al triángulo formado por los 3 pies de las alturas.

Dibujamos la recta perpendicular a la bisectriz del vértice  que pasa por .

Dibujamos la recta perpendicular a la bisectriz del vértice  que pasa por .

Dibujamos la recta perpendicular a la bisectriz del vértice  que pasa por .

Las intersecciones (dos a dos) de estas perpendiculares forman el triángulo .

 

Figure barroso231.fig

Applet created on 2/04/05 by Ricard Peiró with CabriJava